Схемы Бернулли с конечным алфавитом
Здесь нас интересуют последовательности очень длинных слов \((x_0,x_1,x_2,\ldots)\), где каждый \(x_i\) берётся из конечного алфавита \(\mathcal A:=\{a,b,\ldots\}\). Мы будем рассматривать бесконечно длинные слова, что является стандартным подходом, если длина слова значительно превышает число итераций отображения сдвига (определённого ниже). Эти структуры являются базовым строительным блоком для статистической механики, динамических систем и конечных автоматов. Здесь мы рассмотрим простейший пример — случай, когда каждая буква выбирается независимо.
Эта страница содержит интерактивный контент, который вы можете свободно изучать и изменять. Для более сложных изменений рекомендуется запустить и отредактировать интерактивный Jupyter Notebook. Вы можете:
- Запустить его на компьютере с установленным Python/Jupyter-lab (требуются
ipywidgets,numpy,matplotlib). - Запустить его с помощью онлайн-сервиса. Официальный сайт Jupyter предоставляет бесплатный и открытый сервис. Если вам нужна большая вычислительная мощность, вы можете импортировать блокнот в Google Colab (требуется учётная запись Google).
Определения
Пусть \(\mathcal A\) — конечное или счётное множество, и пусть \(M\colon \mathcal A\times \mathcal A\to \{0,1\}\). \(\mathcal A\) представляет собой алфавит, а \(M\) кодирует, какие пары букв могут быть последовательными (более сложные правила для разрешённых последовательностей букв вписываются в эту структуру простым изменением пространства алфавита).
Пространство \(\Sigma \equiv \Sigma(\mathcal A,M)\) \(M\)-совместимых слов — это пространство последовательностей \[ \Sigma:= \left\{ x \in \mathcal A^{\mathbb N} \,:\: M_{x_i,x_{i+1}}=1,\,\forall i\in \mathbb N \right\} \] Другими словами, \(M\) указывает, какие буквы могут идти друг за другом, а \(\Sigma\) — это пространство бесконечно длинных слов, которые содержат только разрешённые последовательные пары букв. \(\Sigma\) является измеримым пространством, будучи измеримым подмножеством \(\mathcal A^{\mathbb N}\) (снабжённого \(\sigma\)-алгеброй произведения). Элементы \(\Sigma\) обычно обозначаются \(x,y,z\), и мы пишем \(x=(x_0,x_1\ldots)\) и так далее.
Определение 1 (Отображение сдвига) Отображение \[ \begin{aligned} & T \colon \Sigma\to \Sigma \\ & (Tx)_i=x_{i+1} \end{aligned} \] называется отображением сдвига.
Обычно пара \((\mathcal A, M)\) (и, следовательно, получающееся пространство \(\Sigma\), оснащённое отображением сдвига \(T\)) называется символической динамической системой.
Заметьте, что \(T\) не является обратимым (если только \(\mathcal A\) не содержит всего один элемент), так как первая буква \(x\) исчезает в \(Tx\), вторая буква становится первой и так далее.
Определение 2 (Инвариантная мера) Вероятностная мера \(\mathbb P\) на \(\Sigma\) называется инвариантной, если \[ \begin{aligned} \mathbb P( E)=\mathbb P(T^{-1}(E)) \end{aligned} \tag{1}\]
Пусть \(\mu \in \mathcal P(\mathcal A)\) — вероятностная мера на \(\mathcal A\). Если \(M_{a,b}=1\) для всех \(a,b\in \mathcal A\), то мера-произведение \(\mathbb P= \mu^{\otimes \mathbb N}\) инвариантна. Это утверждение очевидно, это просто сложный способ сказать, что \[ \mathbb P(X_{0}\in A_0,\ldots, X_{n-1} \in A_{n-1})= \mathbb P(X_{1}\in A_0,\ldots, X_{n} \in A_{n-1}) \] если \(X_i\) являются последовательностью независимых одинаково распределённых (i.i.d.) случайных величин. Действительно, по определению \(\sigma\)-алгебры произведения, достаточно проверить Уравнение 1 для цилиндрических множеств \(E=A_0\times \cdots A_{n-1} \times \mathcal A \times \dots \mathcal A\).
Определение 3 (Схема Бернулли) Схема Бернулли — это символическая динамическая система, где \(\mathcal A\) конечно или счётно, \(M_{a,b}=1\) для всех \(a,b \in \mathcal A\), и \(\mathbb P=\mu^{\otimes \mathbb N}\) — вероятностная мера-произведение на \(\Sigma=\mathcal A^{\mathbb N}\) для некоторой вероятности \(\mu\) на \(\mathcal A\). Другими словами, это просто последовательность i.i.d. случайных величин на конечном или счётном пространстве \(\mathcal A\), каждая с распределением \(\mu\). Если \(\mathcal A\) конечно, то схема называется конечной.
Пример 1 Рассмотрим схему Бернулли над алфавитом \(\mathcal A=\{0,1\}\). Она определяется параметром \(p\in [0,1]\), заданным как \(p=\mu(\{1\})\). Чтобы избежать тривиальных ситуаций, мы выбираем \(p\in (0,1)\). С точностью до счётного множества (и, следовательно, множества \(\mathbb P\)-меры \(0\)), \(\Sigma=\{0,1\}^{\mathbb N}\) находится в биекции с интервалом \([0,1]\) через отображение \[ \Phi(x):= \sum_{i\ge 0} 2^{-i-1} x_i \] Точка \(\Phi(x)\) будет находиться в интервале \([0,1/2)\), если \(x_0=0\), и в интервале \([1/2,1]\), если \(x_0=1\). Аналогично, \(\Phi(x)\in [0,1/4)\), если \(x_0=0\) и \(x_1=0\), \(\Phi(x)\in [1/4,1/2)\), если \(x_0=0\) и \(x_1=1\), и так далее. Это не совсем точно, так как двоично-рациональные числа допускают два двоичных представления, например, \(\Phi(01111111\ldots)=1/2=\Phi(10000000\ldots)\). Но это всего лишь счётное множество, которым мы пренебрежём, так как оно имеет меру \(0\) (можно сделать \(\Phi\) биективным и измеримым, изменив его определение на счётном множестве, но здесь нам это не понадобится).
Таким образом, мы можем вместо этого рассматривать эту схему Бернулли на \([0,1]\). Чему соответствует отображение сдвига \(x\mapsto Tx\)? Другими словами, можем ли мы определить отображение \(T'\colon [0,1]\to [0,1]\) такое, что \(T'(\Phi(x))=\Phi(Tx)\)? Это просто способ сказать: я сначала меняю пространство для представления моих точек, с \(\Sigma \ni x\) на \([0,1] \ni \Phi(x)\). Теперь \(x\) меняется на \(Tx\), могу ли я прочитать это изменение автономно на \([0,1]\), просто как функцию от образа \(\Phi(x)\)? Конечно, можем, так как \(\Phi\) обратимо почти всюду. Итак, \(T'y=\Phi( T \Phi^{-1}y)\). Мы утверждаем, что \(T'y= 2y (\mathrm{mod} 1)\); что легко проверить. Действительно, \[ \Phi(Tx)= \sum_{i\ge 0} 2^{-i-1}x_{i+1}= \begin{cases} 2\Phi(x) & \text{if $x_0=0$} \\ 2\Phi(x) -1 & \text{if $x_0=1$} \end{cases} \]
Конечные схемы
Сосредоточимся на конечных схемах Бернулли. Пусть \(\mathcal A=\{0,1,\ldots,n-1\}\), \(\Sigma=\mathcal A^{\mathbb N}\) и \(p_k:=\mu(\{k\})\), так что \(\sum_i p_i=1\). Мы предполагаем, что \(p_i>0\) (в противном случае просто игнорируем буквы алфавита с вероятностью \(0\)). Как и в Пример 1, рассмотрим \(n\)-ичное представление \[\begin{align*} & \Phi \colon \Sigma \to [0,1] \\ & \Phi(x):= \sum_{i\ge 0} n^{-i-1} x_i \end{align*}\]
Упражнение 1 Докажите, что в этом случае \(n\)-ичное представление переносит отображение сдвига на \(\Sigma\) в отображение \([0,1]\ni y \mapsto n y (\mathrm{mod} 1)\) на \([0,1]\).
Мы хотим ответить на следующий вопрос. Зафиксируем \(\mu\), то есть зафиксируем \(p_0, \ldots, p_{n-1}\). Каков образ меры (pushforward) \(\mathbb P=\mu^{\otimes \mathbb N}\) при отображении на \([0,1]\)? Другими словами, если мы возьмём \((X_i)_{i \ge 0}\) i.i.d. с распределением \(\mu\) (так что \(\mathbb P(X_i=k)=p_k\)), каким будет распределение случайной величины \[ Y= \sum_{i\ge 0} n^{-i-1} X_i \] Сумма в правой части хорошо определена, так что \(Y\) хорошо определена, и мы хотим исследовать её распределение. Обозначим \(\mathbb Q_{\mu}= \mu^{\otimes \mathbb N} \circ \Phi^{-1}\) закон распределения \(Y\), когда \(X_i\) являются i.i.d. с распределением \(\mu\).
Утверждение 1 Если \(p_k\equiv p=1/n\), то есть если \(X_i\) равномерно распределены на конечном множестве \(\mathcal A\), то \(\mathbb Q_\mu\) является мерой Лебега (но определённой на борелевской \(\sigma\)-алгебре) на \([0,1]\).
Доказательство (Утверждение 1). Действительно, зафиксируем интервал вида \(I= [kn^{-j},(k+1)n^{-j}]\), для некоторого \(j\ge 1\) и \(0\le k\le n^{j}-1\). Мы будем иметь, что \(Y=\Phi(X)\in I\) тогда и только тогда, когда \(\sum_{i=0}^{j-1} n^{-i-1}X_i=kn^{-j}\) (с точностью до счётного множества меры \(0\)). В свою очередь, это верно для единственного значения \((X_0,\ldots,X_{j-1})\). Следовательно, \[ \mathbb Q_\mu(I)= \mathbb P(Y\in I)= \mathbb P\left(\sum_{i=0}^{j-1} n^{-i-1}X_i=kn^{-j}\right)= p^{j}= n^{-j}=\mathrm{Leb}(I) \] Поскольку интервалы такого типа полностью определяют меру, мы имеем \(\mathbb Q_\mu=\mathrm{Leb}\).
Другими словами, мы можем получить меру Лебега, просто подбрасывая монету счётное число раз — довольно интуитивная конструкция для объекта, который был плохо определён до начала 20-го века. Согласно закону больших чисел, Утверждение 1 означает, что для почти всех по Лебегу вещественных чисел частота каждой цифры одинакова. Скажем, если мы зафиксируем \(n=10\), тогда определим \(\eta_{k,\ell}(x)\) как количество раз, которое цифра \(k=0,1,2,3,4,5,6,7,8,9\) встречается в представлении \(x\) в основании 10, в первых \(\ell\) цифрах \(x\). Тогда \[ \mathrm{Leb}\left(\left\{x\in [0,1] \,:\: \limsup_\ell \frac{\eta_{k,\ell}}{\ell} =\liminf_\ell \frac{\eta_{k,\ell}}{\ell} = \frac{1}{10} \right\} \right)=1 \] Действительно, как только мы вернёмся к \(n=10\)-ичному представлению, \(\eta_{k,\ell}\) есть не что иное, как сумма \(\sum_{i=0}^{\ell-1} \mathbf{1}_{X_i=k}\), которая является суммой i.i.d. случайных величин с математическим ожиданием \(1/n\). Таким образом, усиленный закон больших чисел подразумевает, что предел существует и равен \(1/10\) с вероятностью \(1\).
Теорема 1 Для вероятности \(\mu\in \mathcal P(\mathcal A)\), \(\mu(\{k\}):=p_k\) на конечном алфавите \(\mathcal A=\{0,\ldots,n-1\}\), определим \[ E_\mu:= \left\{x\in [0,1] \,:\: \limsup_\ell \frac{\eta_{k,\ell}}{\ell}= \liminf_\ell \frac{\eta_{k,\ell}}{\ell}= p_k, \quad \forall k \in \mathcal A \right\} \] Тогда \(E_\mu\) являются измеримыми, непересекающимися множествами и \(\mathbb Q_\mu(E_\mu)=1\) (и, следовательно, \(\mathbb Q_\mu(E_{\mu'})=0\) для \(\mu \neq \mu'\)). Таким образом,
- Если \(\mu\) равномерна, \(p_k=1/n\), то \(\mathbb Q_\mu\) является мерой Лебега.
- Если существует \(k\in \mathcal A\) такое, что \(p_k=1\), то \(\mathbb Q_\mu\) является мерой Дирака (сосредоточена в одной точке).
- Если \(p_k<1\) для всех \(k\), но мера не является равномерной, то \(\mathbb Q_\mu\) имеет канторовский тип, а именно, она присваивает меру \(0\) каждой точке, но сингулярна относительно меры Лебега.
Доказательство оставлено в качестве упражнения с указаниями.
Упражнение 2
- Заметьте, что по самому своему определению \(E_\mu\) являются борелевски-измеримыми и непересекающимися.
- Рассуждая как в тексте после Утверждение 1, докажите в деталях, что \(\mathbb Q_\mu(E_\mu)=1\).
- Вспомните Утверждение 1 и решите тривиальный случай, когда \(p_k=1\) для некоторого \(k\), чтобы доказать утверждения A) и B) в теореме.
- В случае C) остаётся доказать, что \(\mathbb Q_\mu\) присваивает меру \(0\) каждой точке.
Проверка сходимости
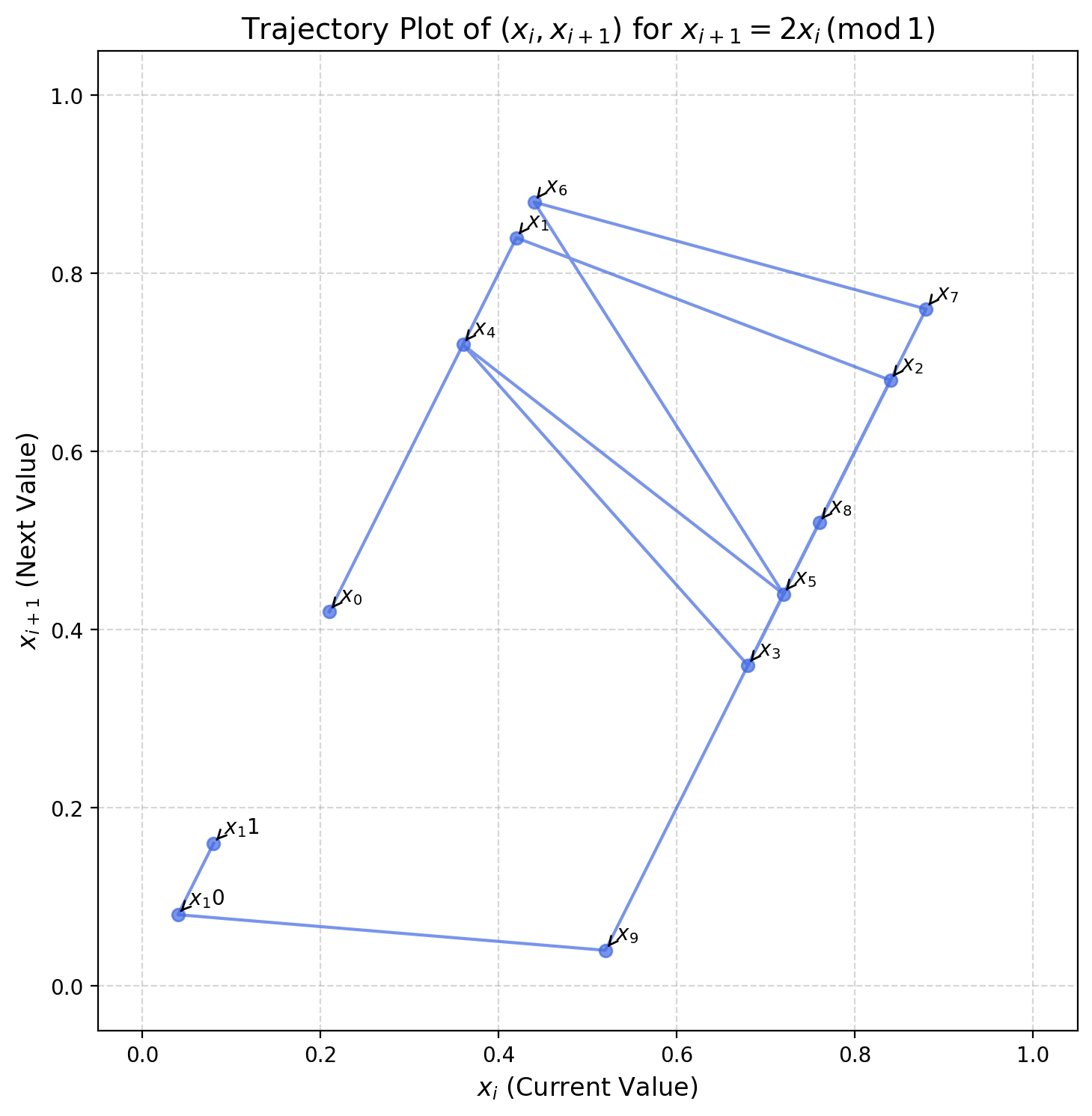
Мы можем посмотреть на траекторию точек карты \(x\mapsto nx (\pmod 1)\).
#| '!! shinylive warning !!': |
#| shinylive does not work in self-contained HTML documents.
#| Please set `embed-resources: false` in your metadata.
#| standalone: true
#| components: [editor, viewer]
#| viewerHeight: 1080
#| editorHeight: 240
#| layout: vertical
from shiny import App, render, ui, reactive, req
import numpy as np
import matplotlib.pyplot as plt
# ========= 1. UI DEFINITION =========
# The UI remains exactly the same.
app_ui = ui.page_sidebar(
ui.sidebar(
ui.h4("Iteration Graph"),
ui.input_slider("n", "Multiplier (n):", min=2, max=10, value=2, step=1),
ui.input_slider("iterations", "Number of Steps:", min=1, max=20, value=10, step=1),
ui.input_slider("x0", "Initial Value (x0):", min=0.0, max=1.0, value=0.21, step=0.01),
ui.input_action_button("generate_button", "Generate Graph", class_="btn-success"),
ui.hr(),
ui.input_checkbox("save_plot", "Save Plot", value=False),
ui.panel_conditional(
"input.save_plot",
ui.input_text("filename", "Filename:", value="graph.png"),
),
title="Controls",
),
ui.output_plot("map_plot", height="600px"),
title="Plot of pairs (x_{i},x_{i+1})",
)
# ========= 2. SERVER LOGIC =========
def server(input, output, session):
# This reactive.Value still acts as the bridge between the action and the render output.
figure_to_display = reactive.Value(None)
def generate_map_sequence(n, num_iterations, x0):
"""Generates a sequence using the map x_{i+1} = n*x_i (mod 1)."""
seq = np.zeros(num_iterations + 1)
seq[0] = x0
for i in range(num_iterations):
seq[i+1] = (n * seq[i]) % 1.0
return seq
# This is the corrected way to perform an action when a button is clicked.
# @reactive.event specifies the trigger.
# @reactive.Effect specifies that this function performs a side-effect.
@reactive.Effect
@reactive.event(input.generate_button, ignore_init=True)
def _():
"""This function runs ONLY when the generate_button is clicked."""
n = input.n()
num_iterations = input.iterations()
x0 = input.x0()
try:
sequence = generate_map_sequence(n, num_iterations, x0)
x_points = sequence[:-1]
y_points = sequence[1:]
fig, ax = plt.subplots(figsize=(8.5, 8.5))
ax.plot(x_points, y_points, 'o-', color='royalblue', markersize=6, alpha=0.7)
for i in range(num_iterations):
ax.annotate(f'$x_{i}$',
xy=(x_points[i], y_points[i]),
xytext=(5, 5),
textcoords='offset points')
ax.set_title(f'Trajectory Plot of $(x_i, x_{{i+1}})$ for $x_{{i+1}} = {n} x_i \\, (\\mathrm{{mod}}\\,1)$', fontsize=12)
ax.set_xlabel('$x_i$ (Current Value)', fontsize=12)
ax.set_ylabel('$x_{i+1}$ (Next Value)', fontsize=12)
ax.set_xlim(-0.05, 1.05)
ax.set_ylim(-0.05, 1.05)
ax.set_aspect('equal', adjustable='box')
ax.grid(True, linestyle='--', alpha=0.5)
if input.save_plot():
req(input.filename(), cancel_output=True)
fig.savefig(input.filename(), dpi=400)
# Set the reactive value, which will cause the plot output to update.
figure_to_display.set(fig)
except Exception as e:
fig, ax = plt.subplots()
ax.text(0.5, 0.5, f"An error occurred: {e}", ha='center', va='center')
figure_to_display.set(fig)
@output
@render.plot
def map_plot():
# This render function simply displays the figure held in our reactive.Value.
fig = figure_to_display.get()
# Don't render an empty output before the button is first clicked.
req(fig)
return fig
# ========= 3. APP INSTANTIATION =========
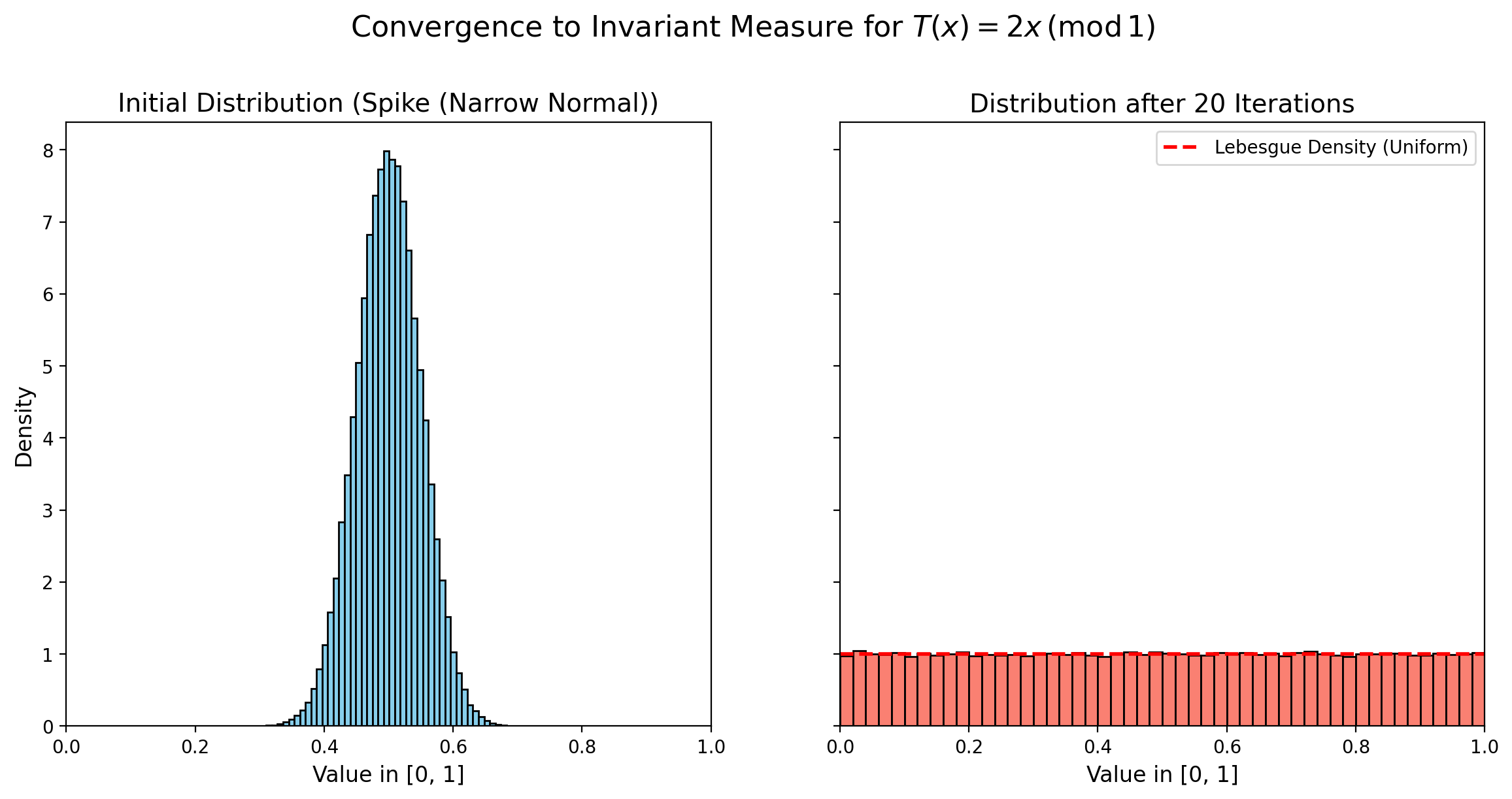
app = App(app_ui, server)Мы можем проверить, что если начать с \(N\) точек, выбранных с заданным распределением \(\mu\), то можно численно увидеть, что через несколько шагов они рассредоточатся по интервалу. Идея заключается в том, что если начать с распределения \(\mu\), абсолютно непрерывного относительно инвариантной меры, то после множества итераций отображения сдвига \(T\) распределение точек приблизится к инвариантной мере (мере Лебега).
Однако мера Лебега — не единственная инвариантная мера, и по мере многократного итерирования отображения мы сталкиваемся с проблемами. Численная точность (тот факт, что мы не можем точно выбрать a.c. относительно Лебега) будет иметь значение при многократном итерировании отображения, например, периодические орбиты (с вероятностью \(0\) относительно Лебега) имеют положительную вероятность при компьютерной выборке. Эффект виден в этом видео.
Не стесняйтесь экспериментировать, как различные распределения сходятся к распределению Лебега. Можете ли вы представить себе, как математически выразить результат сходимости?
#| '!! shinylive warning !!': |
#| shinylive does not work in self-contained HTML documents.
#| Please set `embed-resources: false` in your metadata.
#| standalone: true
#| components: [editor, viewer]
#| viewerHeight: 1080
#| editorHeight: 240
#| layout: vertical
from shiny import App, render, ui, reactive, req
import numpy as np
import matplotlib.pyplot as plt
# ========= 1. UI DEFINITION =========
# The UI is structured with controls in a sidebar and the main plot output.
# The descriptive text below the plot has been removed as requested.
app_ui = ui.page_sidebar(
ui.sidebar(
ui.h4("Simulation Controls"),
ui.input_slider("n_slider", "Multiplier (n):", min=2, max=10, value=2, step=1),
ui.input_slider("num_points_slider", "Number of Points:", min=10000, max=500000, value=100000, step=10000),
ui.input_slider("num_iterations_slider", "Number of Iterations:", min=1, max=50, value=20, step=1),
ui.input_select("distribution", "Initial Distribution:",
choices=['Spike (Narrow Normal)', 'Uniform (Lebesgue)', 'Periodic Points'],
selected='Spike (Narrow Normal)'),
ui.input_action_button("run_button", "Run Simulation", class_="btn-success"),
ui.hr(),
ui.h4("Plotting & Saving"),
ui.input_checkbox("save_plot", "Save Plot", value=False),
ui.panel_conditional(
"input.save_plot",
ui.input_text("filename", "Filename:", value="measure_invariance.png"),
),
title="Controls",
),
ui.output_plot("measure_plot", height="600px"),
title="Convergence to invariant measures",
)
# ========= 2. SERVER LOGIC =========
def server(input, output, session):
figure_to_display = reactive.Value(None)
def generate_and_iterate(dist_name, num_points, n, num_iterations):
"""Generates initial points and iterates the map on all of them."""
if dist_name == 'Uniform (Lebesgue)':
initial_points = np.random.rand(num_points)
elif dist_name == 'Spike (Narrow Normal)':
initial_points = np.mod(np.random.normal(loc=0.5, scale=0.05, size=num_points), 1.0)
elif dist_name == 'Periodic Points':
# Points are concentrated around rational periodic orbits, which converge slowly.
if n == 2:
# For n=2, the orbit {1/3, 2/3} is a classic period-2 orbit.
base_points = [1/3, 2/3]
else:
# For n>2, points k/(n-1) are fixed points (period 1).
base_points = [1/(n-1), 2/(n-1)]
num_bases = len(base_points)
points_per_base = num_points // num_bases
all_samples = []
for i, base in enumerate(base_points):
# Distribute points evenly among bases, giving remainder to the last one.
current_num_points = points_per_base if i < num_bases - 1 else num_points - (points_per_base * (num_bases - 1))
# Create a very narrow spike around the periodic point.
samples = np.random.normal(loc=base, scale=1e-6, size=current_num_points)
all_samples.append(samples)
initial_points = np.mod(np.concatenate(all_samples), 1.0)
np.random.shuffle(initial_points)
else:
raise ValueError(f"Unknown distribution: {dist_name}")
final_points = initial_points.copy()
for _ in range(num_iterations):
final_points = (n * final_points) % 1.0
return initial_points, final_points
@reactive.Effect
@reactive.event(input.run_button, ignore_init=True)
def _():
"""This function runs when the 'Run Simulation' button is clicked."""
n = input.n_slider()
num_points = input.num_points_slider()
num_iterations = input.num_iterations_slider()
dist_name = input.distribution()
try:
initial, final = generate_and_iterate(dist_name, num_points, n, num_iterations)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6), sharey=True)
ax1.hist(initial, bins=50, density=True, color='skyblue', edgecolor='black')
ax1.set_title(f'Initial Distribution ({dist_name})', fontsize=14)
ax1.set_xlabel('Value in [0, 1]', fontsize=12)
ax1.set_ylabel('Density', fontsize=12)
ax1.set_xlim(0, 1)
ax1.grid(True, linestyle='--', alpha=0.5)
ax2.hist(final, bins=50, density=True, color='salmon', edgecolor='black')
ax2.set_title(f'Distribution after {num_iterations} Iterations', fontsize=14)
ax2.set_xlabel('Value in [0, 1]', fontsize=12)
ax2.set_xlim(0, 1)
ax2.axhline(1.0, color='red', linestyle='--', linewidth=2, label='Lebesgue Density (Uniform)')
ax2.legend()
ax2.grid(True, linestyle='--', alpha=0.5)
# fig.suptitle(f'Convergence to Invariant Measure for $T(x) = {n}x \\, (\\mathrm{{mod}}\\,1)$', fontsize=16, y=1.02)
if input.save_plot():
req(input.filename(), cancel_output=True)
fig.savefig(input.filename(), dpi=400, bbox_inches='tight')
figure_to_display.set(fig)
except Exception as e:
fig, ax = plt.subplots()
ax.text(0.5, 0.5, f"An error occurred: {e}", ha='center', va='center', color='red')
figure_to_display.set(fig)
@output
@render.plot
def measure_plot():
"""Renders the plot held in the reactive value."""
fig = figure_to_display.get()
req(fig)
return fig
# ========= 3. APP INSTANTIATION =========
app = App(app_ui, server)