Семинар 1
Задача 1, Сложность 1
Имеются две одинаковые монеты. На одной стороне каждой из них написан \(0\), а на другой \(1\). Монеты подбросили и посчитали сумму выпавших очков. Затем повторили бросок. Какова вероятность, что получилась такая же сумма очков, если
- монеты различимы?
- монеты неразличимы (бозонные)?
Пусть \(S_1, S_2\) — сумма результатов первого и второго подбрасывания. Нам нужно найти \(\mathbb{P}(S_1=S_2) = \sum_{k=0}^2 \mathbb{P}(S_1=k)^2\).
Для различимых монет пространство элементарных исходов — это \(\{(0,0), (0,1), (1,0), (1,1)\}\), где каждый исход имеет вероятность \(1/4\). Вероятности для сумм: \(\mathbb{P}(S=0)=1/4\), \(\mathbb{P}(S=1)=1/2\), \(\mathbb{P}(S=2)=1/4\). \(\mathbb{P}(\text{та же сумма}) = (1/4)^2 + (1/2)^2 + (1/4)^2 = 6/16 = 3/8\).
Для неразличимых (бозонных) монет пространство элементарных исходов — это множество исходов \(\{\{0,0\}, \{0,1\}, \{1,1\}\}\). Предполагая, что они равновероятны, каждый имеет вероятность \(1/3\). Вероятности для сумм: \(\mathbb{P}(S=0)=1/3\), \(\mathbb{P}(S=1)=1/3\), \(\mathbb{P}(S=2)=1/3\). \(\mathbb{P}(\text{та же сумма}) = (1/3)^2 + (1/3)^2 + (1/3)^2 = 3/9 = 1/3\).
Задача 2, Сложность 1
Вместе с другими студентами вы сдаете экзамен. Число студентов равно числу билетов и составляет \(n\). Известно, что среди билетов имеется \(1\le k\le n\) простых. Студенты заходят в аудиторию по очереди, тянут билет и оставляют его себе. Когда вам выгоднее всего зайти, чтобы максимизировать вероятность вытянуть простой билет? Чтобы разобраться в этом животрепещущем вопросе, вычислите вероятность вытянуть простой билет, если вы заходите
- первым;
- \(j\)-ым, \(1\le j \le n\).
По симметрии (инвариантность вероятности каждой последовательности простых/сложных задач относительно перестановок), вероятность не зависит от позиции.
- Для первого студента вероятность очевидно равна \(k/n\).
- Любой из \(n\) билетов равновероятно может оказаться на \(j\)-й позиции. Поскольку \(k\) из них простые, вероятность равна \(k/n\). Время входа не имеет значения.
Задача 3, Сложность 3
Рассматривается случайное размещение \(n\) неразличимых (бозонных) частиц по \(M\) различимым ячейкам. Вычислите вероятность \(Q_k (n; M)\) того, что в фиксированной ячейке содержится \(k\) частиц.
Найдите предел \(Q_k (n; M)\), когда \(n, M \to \infty\) таким образом, что \(n/M \to \lambda\), где \(\lambda>0\) фиксировано.
Примечание: Такое распределение называется “статистикой Бозе-Эйнштейна”; оно описывает распределение бозонов по уровням энергии и дает физическое обоснование модели, в которой неразличимые предметы размещаются в различимых контейнерах.
Общее число конфигураций равно \(\binom{n+M-1}{n}\). Если мы зафиксируем, что в одной ячейке находится \(k\) частиц, мы должны распределить оставшиеся \(n-k\) частиц по остальным \(M-1\) ячейкам. Количество способов это сделать равно \(\binom{(n-k)+(M-1)-1}{n-k} = \binom{n-k+M-2}{n-k}\). \[ Q_k(n; M) = \frac{\binom{n-k+M-2}{n-k}}{\binom{n+M-1}{n}} \]
В пределе эта вероятность сходится к геометрическому распределению с параметром \(p = \frac{\lambda}{\lambda+1}\). \[ \lim_{n,M\to\infty} Q_k(n;M) = (1-p)p^k = \frac{1}{\lambda+1}\left(\frac{\lambda}{\lambda+1}\right)^k \]
Задача 4, Сложность 2
Имеется код длины \(n\), состоящий из цифр от \(0\) до \(9\). Найти вероятность того, что цифры расположены в неубывающем порядке.
Общее число кодов равно \(10^n\). Неубывающая последовательность определяется мультимножеством её цифр. Число таких мультимножеств размера \(n\) из 10 цифр равно \(\binom{n+10-1}{n} = \binom{n+9}{n}\). \[ \mathbb{P}(\text{неубывающая}) = \frac{\binom{n+9}{n}}{10^n} \]
Задача 5, Сложность 1
Из колоды (\(52\) карты) вынимают \(4\) карты.
- Какова вероятность, что все 4 карты — пики?
- Какова вероятность, что 3 карты — пики, а одна — черви?
Напомним, что французская (покерная) колода из \(52\) карт состоит из \(4\) мастей, каждая из которых насчитывает \(13\) номиналов (или значений).
Существует \(\binom{52}{4}\) способов выбрать 4 карты из 52. Существует \(\binom{13}{4}\) способов выбрать пиковые карты. Таким образом, вероятность равна \(\frac{\binom{13}{4}}{\binom{52}{4}}=\frac{13! 48!}{52! 9!}=\frac{13 \cdot 12 \cdot 11 \cdot 10}{52 \cdot 51 \cdot 50 \cdot 49}\approx 0.0026\).
Существует \(\binom{13}{3} \binom{13}{1}\) способов выбрать 3 пиковые карты и одну червовую карту. Таким образом, ответ \(\frac{\binom{13}{3} \binom{13}{1}}{\binom{52}{4}}\approx 0.0137\).
Задача 6, Сложность 3
Имеется три пронумерованных ящика (1,2,3), по ним случайным образом разложены 10 неразличимых (бозонных) белых шаров и 4 пронумерованных красных шара (1,2,3,4). Найдите вероятность того, что в каждом ящике есть хотя бы один белый шар и хотя бы один красный шар с номером, большим номера ящика.
Размещения белых и красных шаров независимы.
- Белые шары: Общее число способов разместить 10 неразличимых шаров в 3 ящика равно \(\binom{10+3-1}{10}=66\). Число способов, при которых в каждом ящике есть хотя бы один шар, равно \(\binom{10-1}{3-1}=\binom{9}{2}=36\). Таким образом, \(p_W = 36/66 = 6/11\).
- Красные шары: Общее число способов разместить 4 различимых шара равно \(3^4=81\). Условие требует, чтобы шар \(R_2\) был в ящике 1, \(R_3\) — в ящике 2, а \(R_4\) — в ящике 3. Шар \(R_1\) может находиться в любом из 3 ящиков. Это дает 3 благоприятных размещения. Таким образом, \(p_R = 3/81 = 1/27\).
В силу независимости искомая вероятность равна \(p_W p_R = \frac{6}{11} \times \frac{1}{27} = \frac{2}{99}\).
Задача 7, Сложность 3
Имеется три ящика, в них случайным образом лежат три черных и три белых шара. Найдите вероятность того, что в первом ящике лежит не менее двух черных шаров, а в третьем — не более одного белого, если
- шары пронумерованы
- шары отличаются только цветом (бозонные).
Пусть A — событие для черных шаров, а B — для белых. События независимы.
-
Пронумерованные шары: Общее число способов для каждого цвета — \(3^3=27\).
- \(\mathbb{P}(A)\): Благоприятные способы для \(B_1 \ge 2\): \(\binom{3}{2} \cdot 2^1 + \binom{3}{3} \cdot 2^0 = 7\). Так что \(\mathbb{P}(A)=7/27\).
- \(\mathbb{P}(B)\): Благоприятные способы для \(W_3 \le 1\): \(2^3 + \binom{3}{1} \cdot 2^2 = 20\). Так что \(\mathbb{P}(B)=20/27\).
- \(\mathbb{P}(A \cap B) = \mathbb{P}(A)\mathbb{P}(B) = \frac{7}{27} \frac{20}{27} = \frac{140}{729}\).
-
Бозонные шары: Общее число способов для каждого цвета — \(\binom{3+3-1}{3}=10\).
- \(\mathbb{P}(A)\): Конфигурации \((b_1,b_2,b_3)\) для \(b_1 \ge 2\): \((2,1,0), (2,0,1), (3,0,0)\). 3 благоприятных способа. \(\mathbb{P}(A)=3/10\).
- \(\mathbb{P}(B)\): Конфигурации для \(w_3 \le 1\): (4 с \(w_3=0\)) + (3 с \(w_3=1\)) = 7 способов. \(\mathbb{P}(B)=7/10\).
- \(\mathbb{P}(A \cap B) = \mathbb{P}(A)\mathbb{P}(B) = \frac{3}{10} \frac{7}{10} = \frac{21}{100}\).
Задача 8, Сложность 2
Имеется ящик с 30 различимыми шарами, среди которых 10 красных и 20 черных шаров. Наугад вынимают 12 (без учета порядка и без возвращения). Найдите вероятность того, что среди вынутых шаров оказалось поровну красных и черных. Что изменится, если учитывать порядок?
Нам нужна вероятность вытянуть 6 красных и 6 черных шаров.
- Без учета порядка: Вероятность дается мультивариантным гипергеометрическим распределением \(\mathbb{P}(\text{6К, 6Ч}) = \frac{\binom{10}{6} \binom{20}{6}}{\binom{30}{12}} \approx 0.0941\).
- С учетом порядка: Ничего не меняется. Просто добавились 12 долларов в числителе и знаменателе.
Задача 9, Сложность 3
Так работает (одномерная) линия передачи сотовой сети. \(n\) антенн выстроены в линию на равном расстоянии, каждая повторяет сигнал, полученный от соседней антенны. Сигнал может преодолевать расстояние двух антенн, поэтому передача работает, если нет двух последовательных неисправных антенн. Предположим, что \(m < n\) антенн неисправны, но мы не знаем их положения. Какова вероятность того, что трансмиссия сработает?
- \(\mathrm{I I X I I I X I}\) = работает
- \(\mathrm{I I X X I I I I}\) = не работает
Обозначим ‘I’ для работающей антенны и ‘X’ для неисправной. Чтобы определить конфигурацию работающих-неработающих антенн, достаточно указать положение \(m\) ‘X’ из \(n\) возможных позиций. Таким образом, у нас есть \(\binom{n}{m}\) равновероятных возможностей.
Сколько из них не имеют двух последовательных ‘X’? Чтобы посчитать, нарисуем следующую картину: \[ \mathrm{\_ \,I \,\_ \,I \,\_ \,I \ldots \_ \,I\, \_} \] где имеется \((n-m)\) ‘I’. Чтобы создать рабочую конфигурацию, мы можем разместить \(m\) неисправных антенн в любое из \(n-m+1\) свободных мест, отмеченных ‘_’. Таким образом, вероятность работающей сети равна \[ \frac{\binom{n-m+1}{m}}{\binom{n}{m}} \] что, конечно, означает \(0\) при \(2m > n+1\).
Задача 10, Сложность 3
Человек многократно подбрасывает монету. Он останавливается, как только получает последовательность из \(n\) орлов или последовательность из 1 решки и \((n-1)\) орлов подряд.
- Какова вероятность, что он остановится?
- Какова вероятность, что он остановится на последовательности из n орлов?
Человек остановится с вероятностью 1.
Существует только один способ увидеть последовательность из \(n\) орлов подряд до появления последовательности из 1 решки и \((n-1)\) орлов: эта последовательность должна появиться с самого начала. Таким образом, искомая вероятность равна \(2^{-n}\). В общем случае, для двух заданных последовательностей орлов и решек (или 0 и 1), трудно точно вычислить вероятность того, что одна появится раньше другой. Очевидно, что это зависит не только от длины последовательности, что и показывает данная задача.
Задача 11, Сложность 4
Электричка состоит из \(n\) вагонов. Каждый из \(k\) пассажиров выбирает вагон наудачу. Какова вероятность, что в каждом вагоне будет хотя бы один пассажир? Какова вероятность, что будут заняты ровно \(r\) вагонов?
Если \(E\) — это множество пассажиров, а \(F\) — множество вагонов, задача сводится к вычислению некоторых комбинаторных свойств функций \(f\colon E\to F\) (распределений пассажиров по вагонам). Поскольку \(|E|=k\) и \(|F|=n\), существует \(n^k\) всего функций \(f\colon E \to F\).
Здесь нам нужно посчитать, сколько существует сюръективных функций \(f\colon E\to F\). Предположим, \(k\ge n\) (иначе ответ \(0\)). Для \(A\subset F\) определим \[ \text{Число функций с образом в } A = |A|^k \] По принципу включений-исключений, число функций, имеющих в качестве образа ровно \(F\), равно: \[ \text{Число сюръективных функций} = \sum_{j=0}^n (-1)^{n-j} \binom{n}{j} j^k \] Чтобы найти вероятность, просто разделите на \(n^k\).
Нам нужно посчитать, сколько функций имеют образ мощностью \(r\). Сначала мы выбираем \(r\) вагонов, которые будут заняты, \(\binom{n}{r}\) способами. Затем мы считаем количество сюръективных функций от \(k\) пассажиров к этим \(r\) вагонам. Из предыдущего пункта это \(\sum_{j=0}^r (-1)^{r-j}\binom{r}{j}j^k\). Общее число способов равно: \[ \binom{n}{r} \sum_{j=0}^r (-1)^{r-j}\binom{r}{j}j^k \] Разделите на \(n^k\), чтобы получить вероятность.
Задача 12, Сложность 4
Пассажиры в автобусе рассаживаются случайным образом, не обращая внимания на места, указанные в билете. Число пассажиров равно числу мест. Какова вероятность, что ни один не сядет на свое место?
Пусть \(n\) — число пассажиров и мест. Общее число перестановок равно \(n!\). Мы хотим посчитать перестановки без неподвижных точек (беспорядки). Пусть \(A_i\) — это множество перестановок, где пассажир \(i\) сидит на своем месте. Мы хотим найти \(n! - |\cup_{i=1}^n A_i|\). По принципу включений-исключений: \[ |\cup_{i=1}^n A_i| = \sum_{i} |A_i| - \sum_{i<j} |A_i \cap A_j| + \dots + (-1)^{n-1} |A_1 \cap \dots \cap A_n| \] Размер пересечения \(k\) таких множеств — это число перестановок, где \(k\) конкретных пассажиров находятся на своих местах, что равно \((n-k)!\). Существует \(\binom{n}{k}\) таких пересечений. \[ |\cup_{i=1}^n A_i| = \sum_{k=1}^{n} (-1)^{k-1} \binom{n}{k} (n-k)! = \sum_{k=1}^{n} (-1)^{k-1} \frac{n!}{k!} \] Число беспорядков равно \(D_n = n! - |\cup_{i=1}^n A_i| = n! - \sum_{k=1}^{n} (-1)^{k-1} \frac{n!}{k!} = n! \sum_{k=0}^{n} \frac{(-1)^k}{k!}\). Вероятность равна: \[ \mathbb{P}(\text{никто не на своем месте}) = \frac{D_n}{n!} = \sum_{k=0}^{n} \frac{(-1)^k}{k!} \] При \(n \to \infty\) эта вероятность сходится к \(e^{-1}\).
Задача 13, Сложность 3
Человек одновременно купил две коробки спичек и положил их в карман. После этого каждый раз, когда ему нужно было зажечь спичку, он доставал наудачу ту или иную коробку. Через некоторое время, вытащив одну из коробок, человек обнаружил, что она пуста. Какова вероятность, что в другой коробке в этот момент находилось \(k\) спичек, если число спичек в новой коробке равно \(n\)?
Для определенности, скажем, что вначале в каждом кармане было по \(n\) спичек. Вычислим вероятность того, что человек обнаружит правый карман пустым, и в этот момент в левом кармане будет \(k\) спичек. Чтобы это произошло, он должен был выбрать правый карман \(n\) раз из \(n+(n-k) = 2n-k\) попыток, а затем он должен снова выбрать правый карман на \((2n-k+1)\)-й попытке. Число таких последовательностей выборов равно \(\binom{2n-k}{n}\). Каждая такая последовательность имеет вероятность \((1/2)^{2n-k+1}\). Таким образом, эта вероятность равна \(\binom{2n-k}{n} (\frac{1}{2})^{2n-k+1}\). Искомая вероятность вдвое больше, так как первым может опустеть и левый карман, следовательно, она равна \(\binom{2n-k}{n} 2^{-(2n-k)}\).
Задача 14, Сложность 3
По схеме случайного выбора с возвращением из множества натуральных чисел \(\{1,\dots,N\}\), \(N\ge 2\), выбираются числа \(\xi\) и \(\eta\). Покажите, что \[ \mathbb{P}\left(\xi^2-\eta^2 \text{ кратно 2}\right) < \mathbb{P}\left(\xi^2-\eta^2 \text{ кратно 3}\right) \]
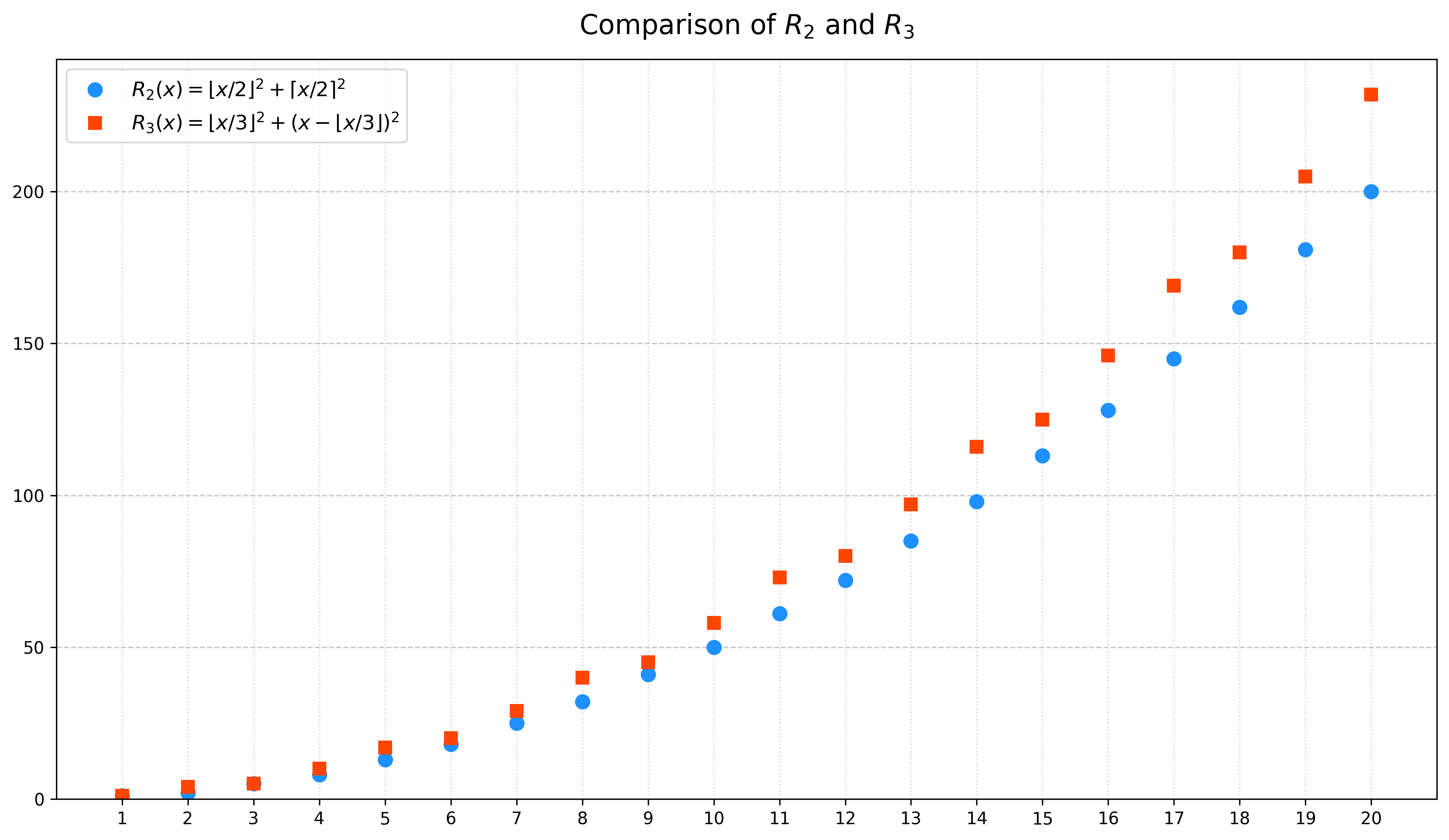
Пусть \(R_k\) — количество пар \((i,j)\), \(1\le i,j \le N\), таких что \(i^2 \equiv j^2 \pmod k\). Нам нужно доказать, что \(R_2 < R_3\), поскольку вероятности получаются делением обеих сторон на \(N^2\).
- Делимость на 2: \(i^2-j^2 = (i-j)(i+j)\) делится на \(2\) тогда и только тогда, когда \(i\) и \(j\) имеют одинаковую четность. Таким образом, \(R_2= \lfloor N/2 \rfloor^2 + \lceil N/2 \rceil^2\).
- Делимость на 3: Для целого числа \(z\), \(z^2 \pmod 3\) может быть либо \(0\), либо \(1\). Следовательно, \(3\) делит \(\xi^2-\eta^2\) тогда и только тогда, когда \(\xi\) и \(\eta\) либо оба делятся на 3, либо оба не делятся на 3. Таким образом, \(R_3= \lfloor N/3 \rfloor^2 + (N - \lfloor N/3 \rfloor)^2\).
- Для больших \(N\), \(R_2 \approx N^2/2\) и \(R_3 \approx 5 N^2/9\). Так как \(5/9 > 1/2\), неравенство очевидно выполняется для достаточно больших \(N\). С помощью элементарного анализа можно показать, что оно выполняется для \(N\ge 2\).
Задача 15, Сложность 4
По схеме случайного выбора с возвращением из множества натуральных чисел \(\{1,\dots,N\}\), \(N\ge 3\), выбираются числа \(\xi\) и \(\eta\). Что больше, \(\mathbb{P}\left(\xi^3+\eta^3 \text{ кратно } 3 \right)\) или \(\mathbb{P}\left(\xi^3+\eta^3 \text{ кратно } 7 \right)\)?
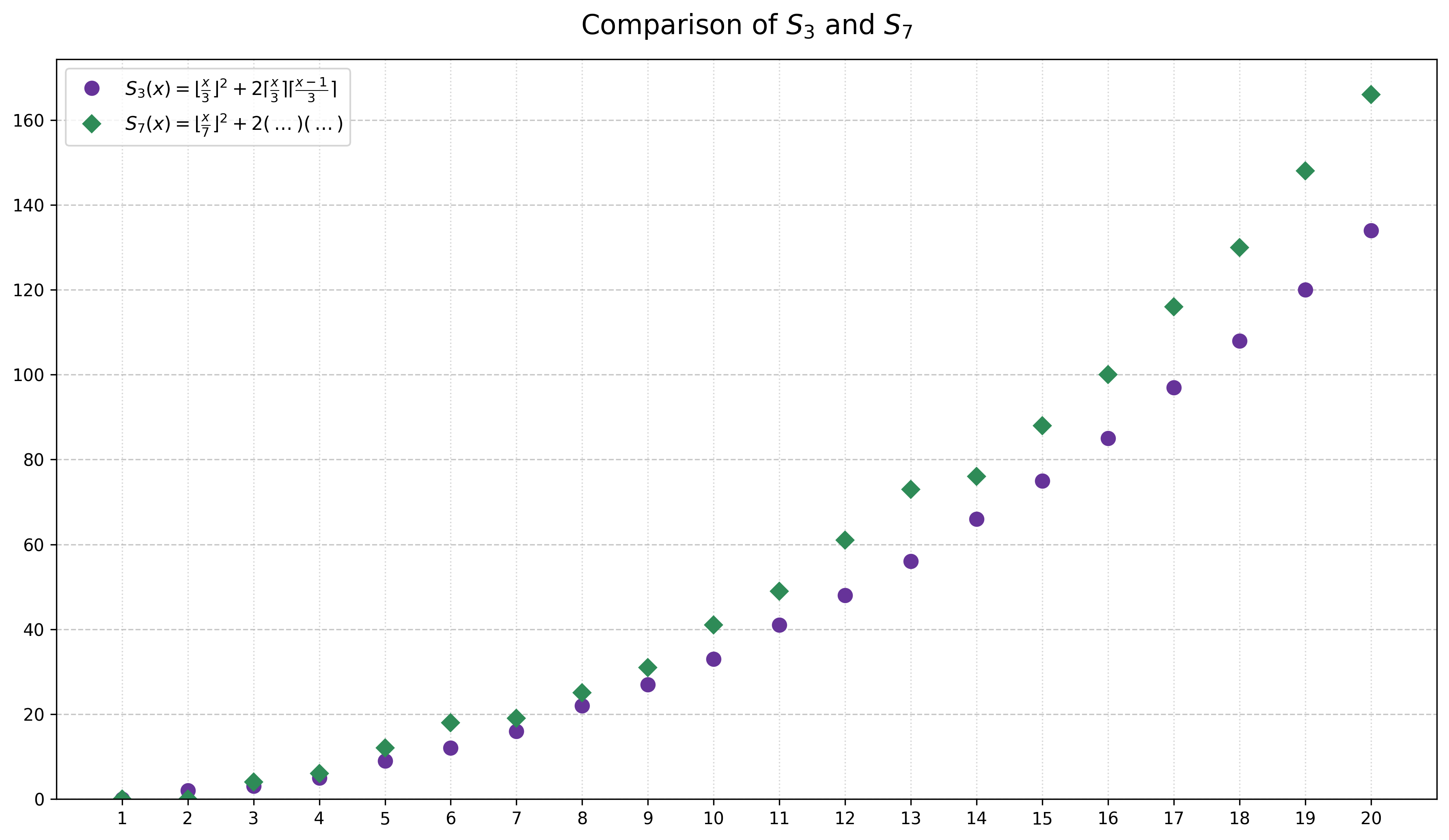
Пусть \(S_{k} := N^2 \mathbb{P}(\xi^3+\eta^3 \equiv 0 \pmod k)\) — количество пар \((i,j)\) таких, что \(i^3+j^3 \equiv 0 \pmod k\), где \(1 \le i,j\le N\).
- Делимость на 3: Кубические вычеты \(x^3\) по модулю 3: \((0^3,1^3,2^3) \equiv (0,1,2) \pmod 3\) (что является следствием Малой теоремы Ферма \(x^p \equiv x \pmod p\)). Таким образом, \(\xi^3+\eta^3 \equiv \xi+\eta \pmod 3\) равно \(0 \pmod 3\) тогда и только тогда, когда: либо \(\xi\) и \(\eta\) оба делятся на \(3\), либо одно имеет остаток \(1\), а другое \(2\). Следовательно, \[ S_{3}= \lfloor N/3 \rfloor^2 + 2 \lceil N/3 \rceil \cdot \lfloor (N-1)/3 + 1 \rfloor \]
- Делимость на 7: Кубические вычеты по модулю \(7\): \((0^3, 1^3, \dots, 6^3) \equiv (0, 1, 1, 6, 1, 6, 6) \pmod 7\). Значит, \(\xi^3+\eta^3 \equiv 0\pmod 7\) тогда и только тогда, когда либо \(\xi\) и \(\eta\) оба делятся на \(7\), либо одно имеет остаток \(1\) (в кубе), а другое \(6\). Пусть \(N_i\) - количество чисел в \(\{1,...,N\}\), чей куб дает остаток \(i \pmod 7\). Тогда \(S_7 = N_0^2 + 2 N_1 N_6\).
- Для больших \(N\), \(S_3 \approx N^2/3\), а \(S_7 \approx N^2((1/7)^2 + 2(3/7)(3/7)) = 19 N^2/49\). Так как \(19/49 > 1/3\), неравенство выполняется для достаточно больших \(N\). С помощью элементарного анализа можно показать, что \(\mathbb{P}\left(\xi^3+\eta^3 \text{ кратно } 7 \right)\) больше для \(N\ge 3\).
Задача 16, Сложность 5
Случайные числа \(\xi\) и \(\eta\) выбираются независимо и равномерно в диапазоне \(\{1,\dots,N\}\). Найдите вероятность \(q_N\) того, что \(\xi\) и \(\eta\) взаимно просты. Найдите \(\lim_{N\to\infty}q_N\), интерпретируемую как вероятность того, что два числа взаимно просты.
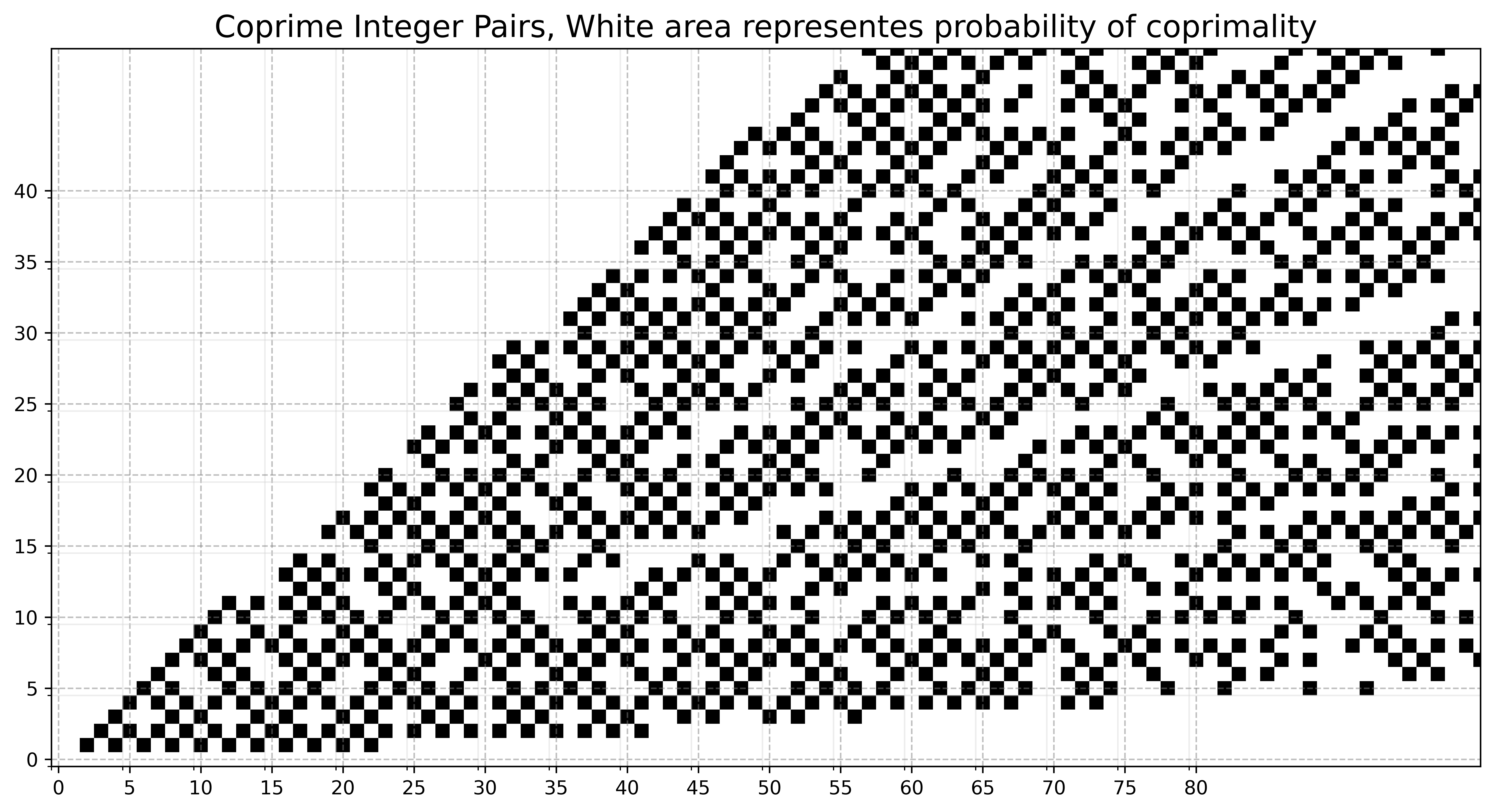
Пусть \(q_N = \mathbb{P}_N(\text{НОД}(\xi,\eta)=1)\). \(A_p\) — событие “\(p\) делит \(\xi\)”, \(B_p\) — событие “\(p\) делит \(\eta\)”. Тогда \[ q_N = \mathbb{P}_N\left( \bigcap_{p \text{ простое}} (A_p \cap B_p)^c \right) \] При больших \(N\) можно неформально предположить, что события \((A_p \cap B_p)\) и \((A_{p'} \cap B_{p'})\) становятся \(\mathbb{P}_N\)-независимыми, а \(A_p\) и \(B_p\) независимы (в точности) для каждого \(N\). Тогда предыдущая формула дает \[ \begin{aligned} q_N & \simeq \prod_{p \text{ простое}} \mathbb{P}_N\left((A_p \cap B_p)^c \right)= \prod_{p \text{ простое}} (1- \mathbb{P}_N(A_p)^2) \\ & \simeq \prod_{p \text{ простое}} (1-1/p^2)= \left( \prod_{p \text{ простое}} \frac{1}{1-p^{-2}}\right)^{-1} = \left( \sum_{n\ge 1} \tfrac{1}{n^2}\right)^{-1}= \frac{6}{\pi^2} \simeq 0.6079 \end{aligned} \]
Чтобы сделать этот аргумент строгим, определим \(E_N:= \{1 \le m,n \le N \,: \text{НОД}(m,n)=1\}\), \(S(N):= |E_N|\). Тогда \(q_N=S(N)/N^2\). Однако \[ S(N):= \sum_{1 \le m,n \le N : \text{НОД}(m,n)=1} 1 = \sum_{d \le N} \mu(d) \left\lfloor \frac{N}{d} \right\rfloor^2 \] где функция Мёбиуса \(\mu(d)\) удовлетворяет \[ \sum_{d} \mu(d) d^{-s} = 1 / \zeta(s) \] Поэтому мы определяем \(\varepsilon_N:= q_N - 6/\pi^2\) и хотим показать, что \(\varepsilon_N\to 0\). Действительно, из приведенного выше обсуждения \[ \varepsilon_N= \sum_{d \le N} \mu(d) \frac{1}{N^2} \left\lfloor \frac{N}{d} \right\rfloor^2 - \sum_{d} \mu(d) d^{-2} \] которое очевидно стремится к нулю при \(N\to \infty\). Можно доказать, что для достаточно больших \(N\ge N_0\) и некоторых констант \(c_{\pm}>0\) \[ c_- \frac{\sqrt{\log \log N}}{N} \le \varepsilon_N \le c_+ \frac{\sqrt{\log \log N}}{N} \]
Дополнительные Задачи
Задача 17, Сложность 2
200 студентов, изучающих теорию вероятностей, делятся на три группы по \(50\), \(50\) и \(100\) человек для посещения семинаров в аудиториях соответствующей вместимости.
- Сколькими способами можно сформировать эти группы студентов?
Александра и Светлана — хорошие подруги и хотели бы оказаться в одной аудитории во время семинара. Но они терпеть не могут Алексея и надеются, что его распределят в другую аудиторию.
- Какова вероятность, что их желания исполнятся?
Это простое упражнение напоминает, что иногда существует несколько различных естественных вероятностных пространств, в которых можно проводить вычисления.
Существует \(\binom{200}{50,50,100}\) способов распределить студентов по трем аудиториям. Однако, если мы рассматриваем способы разделения студентов на две группы по 50 человек и одну группу из 100, то у нас есть \(\binom{200}{50,50,100}/2!\) вариантов.
Существует \(2\binom{197}{48,50,99}\) способов разместить студентов так, чтобы Александра и Светлана были в одной из 50-местных аудиторий, а Алексей — в 100-местной и т.д. Таким образом, искомая вероятность равна \[ \frac{2\binom{197}{48,49,100}+2\binom{197}{48,50,99}+2\binom{197}{49,50,98}}{\binom{200}{50,50,100}} \simeq 0.219 \] Заметим, что мы могли бы эквивалентно рассуждать, распределяя студентов по группам (не различая две группы по 50), что дало бы нам (что, конечно же, то же самое) \[ \frac{\binom{197}{48,49,100}+\binom{197}{48,50,99}+\binom{197}{49,50,98}}{\binom{200}{50,50,100}/2!} \]
Задача 18, Сложность 5
В урне находятся \(u_1\) шаров цвета \(1\), \(u_2\) шаров цвета \(2\), …, \(u_R\) шаров цвета \(R\). Мы производим \(n\) случайных извлечений, и сразу после каждого извлечения шар возвращается в урну вместе с \(m\) другими шарами того же цвета (\(m\ge -1\) и \(n\le u_1+\ldots+ u_R\), если \(m=-1\)).
- Какова вероятность того, что на \(i\)-м извлечении будет вытянут шар цвета \(r\)?
- Какова вероятность того, что среди \(n\) выбранных шаров цвет \(1\) встретится \(j_1\) раз, цвет \(2\) — \(j_2\) раз, \(\ldots\), цвет \(R\) — \(j_R\) раз?
- Пусть \(u_1=u_2=\ldots=u_R=u\). Вычислите предыдущую вероятность в следующих случаях: \(m=-1\) (извлечение без возвращения); \(m=0\) (извлечение с возвращением).
Вероятность вытянуть шар цвета \(r\) на любом конкретном извлечении \(i\) равна \(u_r/U\), где \(U = \sum_r u_r\). Действительно, вероятность любой последовательности цветов не зависит от порядка цветов в ней.
Для конкретной последовательности извлечений с количеством шаров \(j_1, \dots, j_R\) вероятность равна: \[ P(\text{последовательность}) = \frac{\prod_{r=1}^R \prod_{i=0}^{j_r-1}(u_r+im)}{\prod_{i=0}^{n-1}(U+im)} \] Поскольку любая последовательность с тем же составом цветов имеет ту же вероятность, общая вероятность равна этому значению, умноженному на количество таких последовательностей, \(\binom{n}{j_1, \dots, j_R}\): \[ P(j_1, \ldots, j_R) = \binom{n}{j_1, \dots, j_R} \frac{\prod_{r=1}^R \prod_{i=0}^{j_r-1}(u_r+im)}{\prod_{i=0}^{n-1}(U+im)} \]
-
Пусть \(u_r = u\) для всех \(r\). Тогда \(U=Ru\).
- \(m=0\) (извлечение с возвращением): Получается мультиномиальное распределение. \[ P(j_1, \ldots, j_R) = \binom{n}{j_1, \dots, j_R} \frac{\prod_{r=1}^R u^{j_r}}{(Ru)^n} = \binom{n}{j_1, \dots, j_R} \frac{u^n}{R^n u^n} = \binom{n}{j_1, \dots, j_R} (1/R)^n \]
- \(m=-1\) (извлечение без возвращения): Получается многомерное гипергеометрическое распределение. \[ P(j_1, \ldots, j_R) = \frac{\binom{u}{j_1}\binom{u}{j_2}\cdots\binom{u}{j_R}}{\binom{Ru}{n}} \]