Семинар 4

\[\newcommand{\st}{\, : \:} \newcommand{\ind}[1]{\mathbf{1}_{#1}} \newcommand{\dd}{\mathrm{d}}\]

Если написано “дана/известна случайная величина”, $\xi$ то подразумевается, что известны $\mathbb{P}_\xi, F_\xi, p_\xi$ (если плотность существует). Если вас просят найти распределение $\xi$, то достаточно найти любой из объектов выше.

Задача 1

Дано распределения случайного вектора \[ \begin{array}{c|c|c|c|c|c} \beta\setminus\alpha & -2 & -1 & 0 & 1 & 2 \\ \hline -2 & 1/32 & 1/32 & 1/24 & 1/32 & 1/32\\ \hline -1 & 1/32 & 1/32 & 1/24 & 1/32 & 1/32\\ \hline 0 & 1/24 & 1/24 & 1/6 & 1/24 & 1/24\\ \hline 1 & 1/32 & 1/32 & 1/24 & 1/32 & 1/32\\ \hline 2 & 1/32 & 1/32 & 1/24 & 1/32 & 1/32\\ \end{array} \]

Найти вероятность $P(\alpha=\beta)$.
Найти вероятность $P(\alpha >\beta)$.
Найти вероятность $P(\alpha\leqslant\beta)$.
Найти распределения $\alpha$ и $\beta$.
Верно ли, что $\alpha$ и $\beta$ независимы?
Найти распределение $\alpha+\beta$.
Найти распределение $\alpha\beta$.
Найти распределение случайного вектора с компонентами $\alpha+\beta$ и $\alpha-\beta$.
Найти распределение случайного вектора с компонентами $\alpha+\beta$ и $\alpha\beta$.

Решение

$\mathbb{P}(\alpha=\beta)$ — это сумма вероятностей на главной диагонали: \[ \begin{aligned} \mathbb{P}(\alpha=\beta) = p_{-2,-2} + p_{-1,-1} + p_{0,0} + p_{1,1} + p_{2,2} = \frac{1}{32} + \frac{1}{32} + \frac{1}{6} + \frac{1}{32} + \frac{1}{32} = \frac{4}{32} + \frac{1}{6} = \frac{1}{8} + \frac{1}{6} = \frac{3+4}{24} = \frac{7}{24} \end{aligned} \]
$\mathbb{P}(\alpha > \beta)$ — это сумма всех элементов над главной диагональю. Таблица симметрична, поэтому $\mathbb{P}(\alpha > \beta) = \mathbb{P}(\alpha < \beta) =(1 - \mathbb{P}(\alpha=\beta))/2=17/48$.
$\mathbb{P}(\alpha \le \beta) = 1 - \mathbb{P}(\alpha > \beta) = \frac{31}{48}$.
Чтобы получить распределение $\alpha$, просуммируйте по столбцам: например, $\mathbb{P}(\alpha=-2) = 4 \cdot \frac{1}{32} + \frac{1}{24} = \frac{1}{6}$. В силу симметрии таблицы распределение $\beta$ (сумма по строкам) будет таким же.
Нет, они не независимы, например, $\mathbb{P}(\alpha=-2, \beta=-2) = 1/32 \neq \mathbb{P}(\alpha=-2)\mathbb{P}(\beta=-2) = 1/36$.

Чтобы найти распределения для следующих пунктов, нужно сгруппировать ячейки таблицы (это утомительные, но простые вычисления):

Для $\alpha+\beta$: сгруппируйте ячейки $(i,j)$ с одинаковой суммой $k=i+j$.
Для $\alpha\beta$: сгруппируйте ячейки с одинаковым произведением $k=i \cdot j$.
Для $(\alpha+\beta, \alpha-\beta)$ это биекция с $(\alpha,\beta)$, поэтому каждая запись соответствует одной записи в таблице, т.е. $(\alpha,\beta)=((\alpha+\beta)+(\alpha-\beta),(\alpha+\beta)-(\alpha-\beta))/2$.
Для $(\alpha+\beta, \alpha\beta)$ вычислите совместный закон, разделяя случаи, когда $\alpha$ или $\beta$ обращаются в ноль.

Задача 2 [H]

Даны распределения независимых случайных величин $\xi$ и $\eta$: \[ \begin{array}{c|c|c|c|c|c} \xi & -2 & -1 & 0 & 1 & 2 \\ \hline & 1/4 & 1/8 & 1/4 & 1/8 & 1/4\\ \end{array} \]

\[ \begin{array}{c|c|c|c|c|c} \eta & -2 & -1 & 0 & 1 & 2 \\ \hline & 1/8 & 1/4 & 1/4 & 1/4 & 1/8\\ \end{array} \]

Найти вероятность $P(\xi=\eta)$.
Найти вероятность $P(\xi >\eta)$.
Найти вероятность $P(\xi\leqslant\eta)$.
Найти распределения $\xi+\eta$ и $\xi-\eta$.
Найти распределение $\xi\eta$.
Найти распределение случайного вектора с компонентами $\xi+\eta$ и $\xi-\eta$.
Зависимы ли $\xi+\eta$ и $\xi-\eta$?
Найти распределение случайного вектора с компонентами $\xi+\eta$ и $\xi\eta$.

Решение

$\mathbb{P}(\xi=\eta) = \sum_k \mathbb{P}(\xi=k, \eta=k) = \sum_k \mathbb{P}(\xi=k)\mathbb{P}(\eta=k)= \frac{3}{16}$ в силу независимости.

Аналогично для b, c, d, e, f, h. Вычисления производятся путем рассмотрения $\mathbb{P}(\xi=i, \eta=j) = \mathbb{P}(\xi=i)\mathbb{P}(\eta=j)$ и суммирования вероятностей по соответствующим областям.

Проверим независимость $U=\xi+\eta$ и $V=\xi-\eta$. $\mathbb{P}(U=4, V=0) = \mathbb{P}(\xi=2, \eta=2) \neq \mathbb{P}(V=0)\mathbb{P}(U=4)$. Величины $U$ и $V$ зависимы.

Независимость случайных величин

Задача 3 [H]

Пусть $\xi\sim \mathrm{Uniform}([0,1])$, а $\eta\sim \mathrm{Bernoulli}(1/3)$. Поселите эти случайные величины на одном и том же вероятностном пространстве, так, чтобы они были

независимы
зависимы.

Имеется ввиду, что в нужно придумать вероятностное пространство (свое для каждого из пунктов) и случайную величину $\zeta = (\alpha,\beta)$ на нем, такую что $\mathbb{P}_\alpha = \mathbb{P}_\xi$ и $\mathbb{P}_\eta = \mathbb{P}_\beta$.

Решение

Независимы: Возьмем в качестве вероятностного пространства $\Omega = [0,1] \times [0,1]$ с мерой Лебега. Положим $\alpha(t_1, t_2) = t_1$ и $\beta(t_1, t_2) = \mathbf{1}_{[0, 1/3]}(t_2)$. То же самое можно сделать, взяв $\Omega=[0,1]\times \{0,1\}$.
Зависимы: Возьмем пространство $\Omega = [0,1]$ с мерой Лебега. Положим $\alpha(t) = t$, $\beta(t) = \mathbf{1}_{[0, 1/3]}(t)$.

Задача 4

Пусть вероятностное пространство имеет вид $([0,1], \mathcal{B}([0,1]), \text{Leb})$. Зависимы ли следующие случайные величины?

$\xi(t)=2t$, $\eta(t)=1-t^2$
$\xi(t)=\operatorname{sign}\left[\sin(2\pi t)\right]$, $\eta(t)=\operatorname{sign}\left[\sin(4\pi t)\right]$
$\xi(t)=\operatorname{sign}\left[\sin(2\pi t)\right]$, $\eta(t)=\operatorname{sign}(t-1/3)$?

Решение

Зависимы. Они функционально связаны: $\eta(t) = 1 - (\xi(t)/2)^2$. Если мы знаем значение $\xi(t)$, мы однозначно знаем значение $\eta(t)$. Например, для достаточно малого $\varepsilon>0$, $\mathbb{P}(\xi \le \varepsilon, \eta \le \varepsilon) = 0 \neq \mathbb{P}(\xi \le \varepsilon) \mathbb{P}(\eta \le \varepsilon)>0$.
Независимы. $\mathbb{P}(\xi=1 ,\eta=1)=1/4=\mathbb{P}(\xi=1) \mathbb{P}(\eta=1)$, и этого достаточно, поскольку и $\eta$, и $\xi$ принимают только два значения с положительной вероятностью.
Зависимы. Например, $\mathbb{P}(\xi =+1 | \eta=-1 )=1 > \mathbb{P}(\xi =+1)$.

Задача 5 [H]

Привести пример двух зависимых, но не функционально зависимых дискретных с.в. или объяснить почему такой пример не существует.

Решение

Две случайные величины $\alpha, \beta$ называются функционально зависимыми, если одна является измеримой функцией другой, например, $\beta = f(\alpha)$. Это означает, что зная значение $\alpha$, мы однозначно знаем значение $\beta$. Это, как правило, гораздо более сильное условие, чем просто зависимость. Например, в предыдущей задаче $\xi(t)=\operatorname{sign}\left[\sin(2\pi t)\right]$ и $\eta(t)=\operatorname{sign}(t-1/3)$ зависимы, но не функционально зависимы.

Задача 6 [H]

Верно ли, что если $\xi$, $\eta$ независимы, то и для любой функции $f:\mathbb{R}\to\mathbb{R}$ с.в. $f(\xi)$, $f(\eta)$ независимы?

Решение

Можно даже взять измеримые функции $f,g$. Тогда \[ \mathbb{P}(f(\xi) \in A, g(\eta) \in B) =\mathbb{P}(\xi \in f^{-1}(A), \eta \in g^{-1}(B)) = \mathbb{P}(\xi \in f^{-1}(A)) \mathbb{P}(\eta \in g^{-1}(B))=\mathbb{P}(f(\xi) \in A) \mathbb{P}(g(\eta) \in B) \]

Задача 7 [H]

Верно ли, что если $\xi$, $\eta$ зависимы, то и $\xi^2$, $\eta^2$ обязательно зависимы?

Решение

В общем случае неверно, что из независимости $f(\xi)$ и $g(\eta)$ следует независимость $\xi$ и $\eta$. Например, возьмем $\xi=\eta=2\zeta-1$, где $\zeta \sim \mathrm{Bernoulli}(1/2)$. Тогда $\xi^2=\eta^2=1$ независимы.

Задача 8 [H]

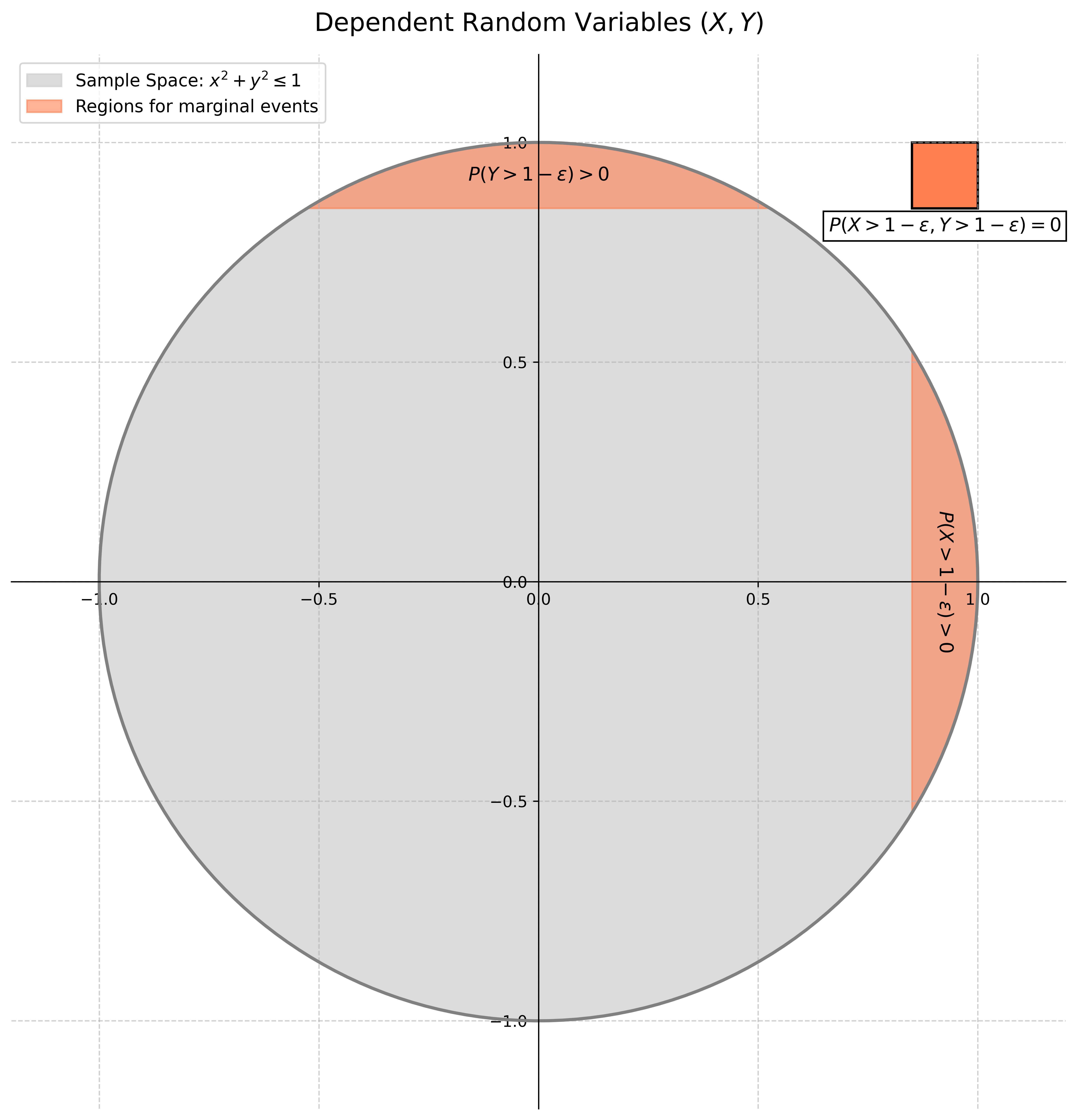
Пусть случайная величина $(\xi,\eta)$ имеет равномерное распределение в ${(x, y) : x^2+y^2 \le 1}$. Являются ли величины $\xi$ и $\eta$ независимыми?

Решение

Нет, например, для достаточно малого $\varepsilon>0$, $\mathbb{P}(\xi \ge 1-\varepsilon, \eta \ge 1-\varepsilon)=0 \neq \mathbb{P}(\xi \ge 1-\varepsilon) \mathbb{P}(\eta \ge 1-\varepsilon)>0$.

Функция распределения

Задача 9

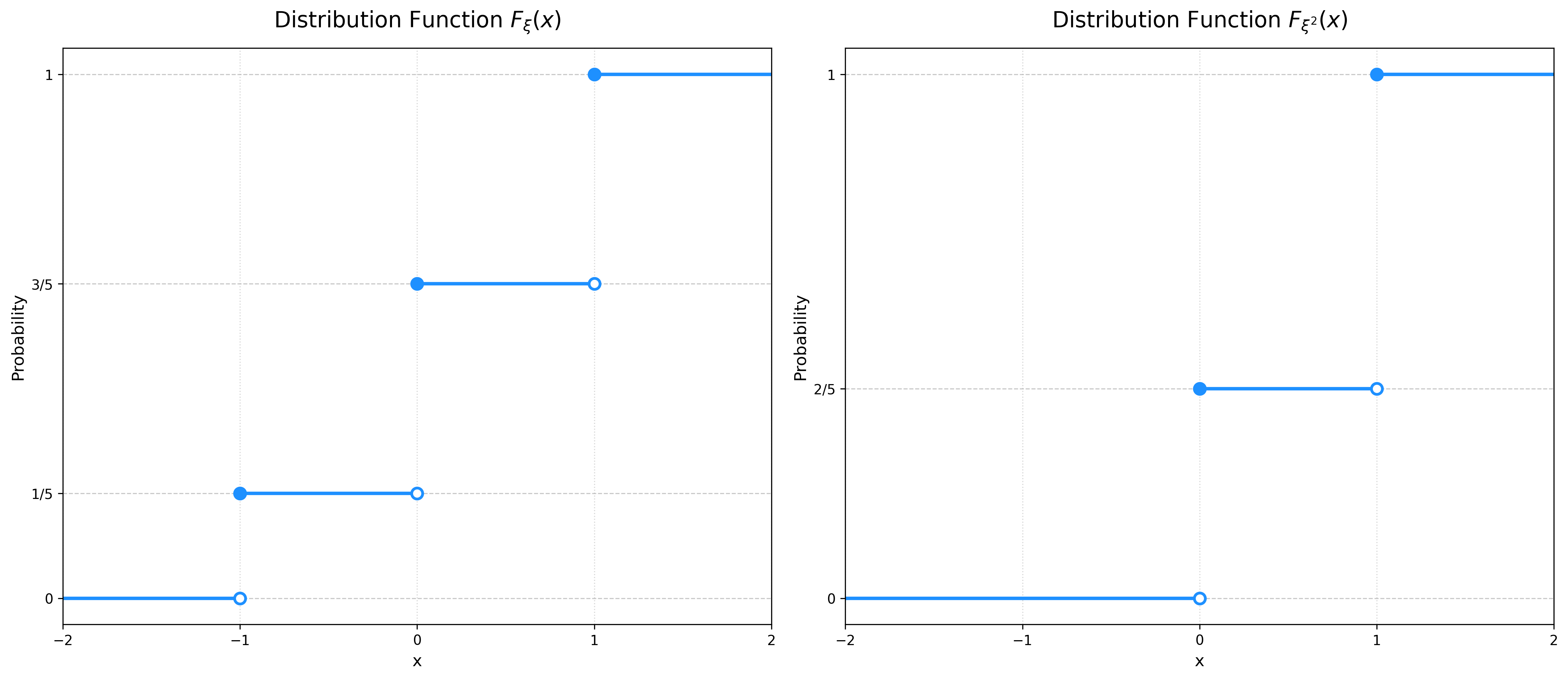
Имеется случайная величина $\xi$ c распределением ниже. Нарисуйте $F_\xi$ и $F_{\xi^2}$. \[ \begin{array}{c|c|c|c} \xi & -1 & 0 & 1 \\ \hline \mathbb{P}_\xi & 1/5 & 2/5 & 2/5 \\ \end{array} \]

Решение

Задача 10 [H]

Нарисуйте функцию распределения $F_\xi$ для $\xi\sim \mathrm{Poisson}(\lambda), \, \lambda>0$.

Решение

Имеем:

$F_\xi(x) = 0$ для $x < 0$.
$F_\xi(x) = e^{-\lambda}$ для $0 \le x < 1$.
$F_\xi(x) = e^{-\lambda}(1+\lambda)$ для $1 \le x < 2$.

и так далее. Функция стремится к 1 при $x \to \infty$.

Задача 11

Стержень длины 2 сломали в случайной точке. Введите явно, с указанием вероятностного пространства, случайную величину $\xi$, дающую длину большего куска из двух получившихся. Найдите $F_\xi$, $F_{\xi^2}$ и плотности $p_\xi$, $p_{\xi^2}$.

Решение

Возьмем $\Omega = [0,2]$ с равномерной мерой. Точка излома $U \sim \mathrm{Uniform}([0,2])$, куски имеют длины $U$ и $2-U$. Таким образом, нас интересует случайная величина $\xi = \max(U, 2-U)$, которая принимает значения в $[1,2]$.

Заметим, что $\xi \le x \iff 2-x \le U \le x$. Таким образом, для $x\in [1,2]$ \[ F_\xi(x)=\int_{2-x}^x \frac{1}{2} du=x-1 \] Значит, $\xi$ равномерно распределена на $[1,2]$, ее плотность постоянна на этом интервале.

Функция распределения $\xi^2$ тогда равна $F_{\xi^2}(x)= \sqrt{x}-1$ для $x\in [1,4]$, а ее плотность - $(2x)^{-1/2} \mathbf{1}_{[1,4]}$.

Задача 12

Даны независимые случайные величины $\xi_1,\dots,\xi_n$. Найдите функцию распределения случайной величины

$\max(\xi_1,\dots,\xi_n)$,
$\min(\xi_1,\dots,\xi_n)$.

Решение

Пусть $F_i(x) = \mathbb{P}(\xi_i \le x)$ - функция распределения для $\xi_i$.

Максимум: Пусть $M_n = \max(\xi_1, \dots, \xi_n)$, тогда $\{M_n \le x\}$ тогда и только тогда, когда все $\xi_i$ не превосходят $x$. Таким образом, в силу независимости: \[ F_{M_n}(x) = \mathbb{P}(M_n \le x) = \mathbb{P}(\xi_1 \le x, \xi_2 \le x, \ldots, \xi_n \le x) = \prod_{i=1}^n F_{i}(x) \] Если все $\xi_i$ одинаково распределены с функцией распределения $F(x)$, то $F_{M_n}(x) = (F(x))^n$.
Минимум: $m_n = \min(\xi_1, \dots, \xi_n)$. В этом случае мы рассуждаем как выше для дополнительного события $m_n>x$, чтобы получить $F_{m_n}(x) = 1 - \prod_{i=1}^n (1 - F_i(x))$. Если все $\xi_i$ одинаково распределены с функцией распределения $F(x)$, то $F_{m_n}(x) = 1 - (1 - F(x))^n$.

Задача 13

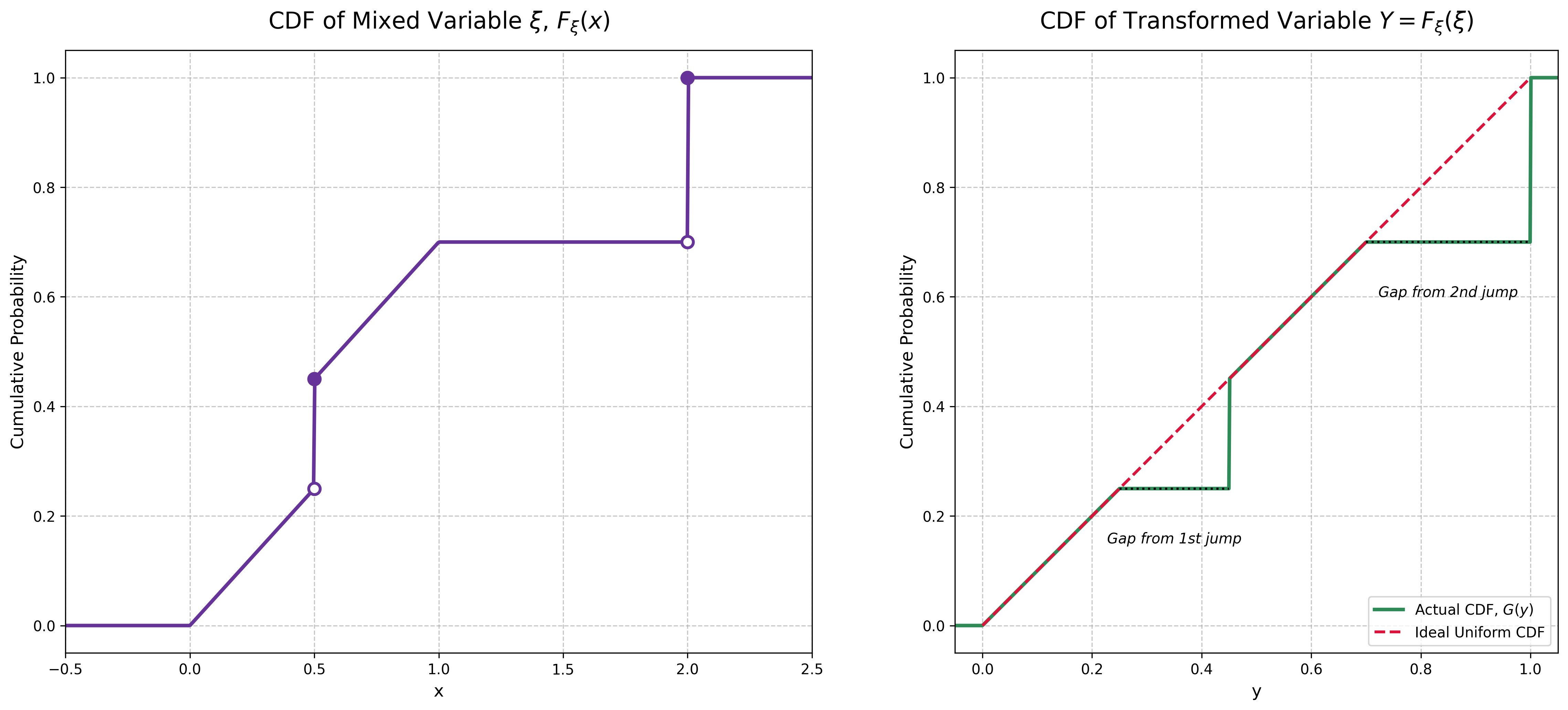
Пусть случайная величина $\xi$ непрерывна (то есть, ее функция распределения $F_\xi$ непрерывна). Найдите распределение случайной величины $F_\xi(\xi)$.

Решение

Обозначим $F=F_\xi$, чтобы напомнить, что это не случайная функция. Пусть $\eta = F(\xi)$. Поскольку $F$ - это функция распределения, ее значения лежат в интервале $[0,1]$. Множество $F^{-1}((-\infty,y])$ является возрастающим (по $y$) замкнутым подмножеством $\mathbb{R}$ вида $F^{-1}((-\infty,y])=(-\infty,s_y]$. Тогда по самому определению $F$ \[ G(y) = \mathbb{P}(\eta \le y)= \mathbb{P}(F(\xi) \le y)= \mathbb{P}(\xi \in F^{-1}((-\infty,y]))= F(s_y) \] Если $F$ непрерывна, то $G(y)=F(s_y)=y$. Таким образом, $F_\xi(\xi)$ является равномерно распределенной случайной величиной. В общем случае, если $F$ не является непрерывной, $G(y)\le y$.

integral transform with jumps — Рисунок 1

Задача 14 [H]

Пусть $\xi\sim \mathrm{Uniform}([-1,1])$. Найдите распределение случайной величины $F_{|\xi|}(\xi)$.

Решение

$|\xi|$ равномерно распределена на $[0,1]$, следовательно $F_{|\xi|}(\xi)= \max(\xi,0)$. Поэтому \[ G(x):= \mathbb{P}(F_{|\xi|}(\xi)\le x)= \begin{cases} 0 & \text{если $x<0$} \\ 1/2+x/2 & \text{если $x\in [0,1]$} \\ 1 & \text{если $x\ge 1$} \end{cases} \]

Задача 15*

(смеси). На вероятностном пространстве $\Omega$ рассматривается следующая конструкция случайной величины $\xi:\mathbb{R}\to\mathbb{R}$ : сначала по равномерной на отрезке $[0,1]$ с.в. $\eta$ выбирают отрезок $[0,\eta(\omega)]$, а потом независимо выбирают случайную величину $\zeta(\omega):=\xi_{\eta(\omega)}(\omega)$ c заданным распределением на отрезке $[0,\eta(\omega)]$. Найти плотность распределения получившейся случайной величины $\xi$, если

$\xi_a \sim \mathrm{Uniform}([0,a])$,
$\xi_a^2 \sim \mathrm{Uniform}([0,a])$.

Решение

\[ \mathbb{P}(\zeta\le x)= \int_0^1 \mathbb{P}(\xi_a \le x)\, da \]

В этом случае последняя формула для $x\in (0,1]$ дает \[ \mathbb{P}(\zeta\le x)= \int_0^1 \tfrac{x}{a} \mathbf{1}_{[0,a)}(x)+ \mathbf{1}_{[a,\infty)}(x) \, da = x-x \log(x) \] что имеет плотность $-\log(x) \mathbf{1}_{(0,1]}(x)$.
В этом случае для $x\in (0,1)$ имеем $\mathbb{P}(\xi_a \le x)=\mathbb{P}(\xi_a^2 \le x^2)= x^2/a \mathbf{1}_{[0,\sqrt{a})}(x)+ \mathbf{1}_{[\sqrt{a},\infty)}(x)$. Поэтому для $x\in (0,1)$ \[ \mathbb{P}(\zeta\le x) = \int_0^1 \tfrac{x^2}{a} \mathbf{1}_{[0,\sqrt{a})}(x)+ \mathbf{1}_{[\sqrt{a},\infty)}(x) da= x^2-2x^2 \log(x) \] и плотность, следовательно, равна $-4x \log(x) \mathbf{1}_{[0,1]}(x)$, что демонстрирует существенно иное поведение в окрестности $x=0$.

Задача 16*

Пусть $\xi\sim \mathrm{Exp}(\lambda)$. Зависимы ли ее целая и дробная части?

Решение

Они независимы. Пусть $X:= \lfloor \xi \rfloor$ - целая часть, а $\eta: = \xi - \lfloor \xi \rfloor$ - дробная часть. Для $k \in \{0,1,2,\dots\}$ и $y \in [0,1)$ вычислим совместное распределение \[ \mathbb{P}(X=k, \eta \le y)=\mathbb{P}(k \le \xi \le k+y)= e^{-\lambda k} - e^{-\lambda (k+y)}= e^{-\lambda k}(1-e^{-\lambda y}) \] Поскольку это произведение функции от $k$ на функцию от $y$, случайные величины независимы. В частности, мы видим, что $X$ имеет геометрическое распределение с параметром (неудачи) $e^{-\lambda}$, в то время как $\eta$ имеет плотность $\lambda e^{-\lambda y}(1-e^{-\lambda})^{-1} \mathbf{1}_{[0,1]}(y)$.

Дополнительные Задачи

Задача 17

Пусть $\xi \colon \Omega \to E$ — случайная величина, а $f\colon E\to F$ — измеримая функция. Здесь $E,F$ — измеримые пространства. Докажите, что $(\xi,f(\xi))$ независимы тогда и только тогда, когда $f(\xi)$ является константой почти наверное (п.н.).

Решение

Если $(\xi,f(\xi))$ независимы, то \[ \mathbb{P}(\xi\in A, f(\xi)\in B)=\mathbb{P}(\xi\in A, \xi \in f^{-1}(B))= \mathbb{P}(\xi\in A) \mathbb{P}(\xi \in f^{-1}(B))=\mathbb{P}(\xi\in A) \mathbb{P}(f(\xi) \in B) \] Если мы теперь выберем $A=f^{-1}(B)$, мы получим $\mathbb{P}(f(\xi)\in B)=\mathbb{P}(f(\xi)\in B)^2$. А именно, $\mathbb{P}(f(\xi)\in B)\in \{0,1\}$ для всех измеримых $B$. Это правильный способ сказать, что $f(\xi)$ является константой. То есть, если $\sigma$-алгебра на $F$ содержит синглтоны, это означает, что $f(\xi)$ является константой п.н. В противном случае, быть константой не определено как измеримое событие, в то время как утверждение, что закон $f(\xi)$ принимает значения в $\{0,1\}$, все еще имеет смысл.