Статистические свойства одномерных случайных блужданий
В этой заметке рассматриваются некоторые особенности одномерного случайного блуждания. Мы рассматриваем случайно блуждающую частицу, которая каждую секунду может сделать шаг вверх с вероятностью \(p\) или шаг вниз с вероятностью \(1-p\). При \(p=1/2\) частица вернётся в начало координат с вероятностью \(1\). Затем можно изучить статистические свойства случайного блуждания, пока частица находится вне \(0\). Некоторые утверждения доказываются разными методами в разных разделах.
Эта страница содержит (в конце) интерактивный контент, который вы можете свободно изучать и изменять. Для более сложных изменений рекомендуется запустить и отредактировать интерактивный Jupyter Notebook. Вы можете:
- Запустить его на компьютере с установленным Python/Jupyter-lab (требуются
ipywidgets,numpy,matplotlib,scipy). - Запустить его с помощью онлайн-сервиса. Официальный сайт Jupyter предоставляет бесплатный и открытый сервис. Если вам нужна большая вычислительная мощность, вы можете импортировать блокнот в Google Colab (требуется учётная запись Google).
Определения
Начнём с формального определения случайного блуждания.
Определение 1 (Одномерное случайное блуждание) Пусть \((X_i)_{i\ge 1}\) — последовательность независимых одинаково распределённых (i.i.d.) случайных величин, таких что \[ \mathbb P(X_i = +1) = p \quad \text{and} \quad \mathbb P(X_i = -1) = 1-p \] для некоторого \(p \in [0,1]\). Одномерное случайное блуждание, начинающееся в начале координат, — это последовательность случайных величин \((S_n)_{n\ge 0}\), определяемая как \(S_0 := 0\) и \[ S_n := \sum_{i=1}^n X_i \quad \text{for } n \ge 1 \tag{1}\] Блуждание называется симметричным, если \(p=1/2\), и асимметричным в противном случае. Мы говорим, что частица возвращается в начало координат в момент времени \(n\), если \(S_n=0\). Время первого возвращения в начало координат — это случайная величина \[ \tau_0 := \inf \{ n \ge 1 \,:\, S_n = 0 \} \tag{2}\] где мы полагаем \(\inf \emptyset = \infty\).
Сначала определим, при каких значениях \(p\) частица наверняка вернётся в начало координат, то есть \(\mathbb P(\tau_0 < \infty) = 1\). Такое блуждание называется возвратным. Если \(\mathbb P(\tau_0 < \infty) < 1\), блуждание называется невозвратным.
Вернётся ли частица в начало координат?
Поведение блуждания кардинально различается в симметричном и асимметричном случаях.
Асимметричный случай: уход на бесконечность
Если блуждание несимметрично (\(p\ne 1/2\)), то существует суммарный дрейф в одном направлении. Усиленного закона больших чисел (УЗБЧ) достаточно, чтобы показать, что частица почти наверное (п.н.) уходит от начала координат навсегда.
Утверждение 1 Если \(p \neq 1/2\), одномерное случайное блуждание является невозвратным. Фактически, \(|S_n| \to \infty\) п.н., что означает, что частица посещает начало координат лишь конечное число раз.
Доказательство (Утверждение 1). Математическое ожидание одного шага равно \(m := \mathbb E[X_i] = 2p-1\). Это \(m\neq 0\) тогда и только тогда, когда \(p \neq 1/2\). Согласно Усиленному закону больших чисел, мы имеем п.н. \[ \lim_{n\to\infty} \frac{S_n}{n} = m \] Это означает, что если \(m\neq 0\), то \(|S_n| \to \infty\) п.н. Следовательно, она может принимать значение \(0\) лишь конечное число раз. Поэтому блуждание является невозвратным.
Примечание. Мы только что проверили, что число возвращений частицы в \(0\) конечно с вероятностью \(1\), если \(p\neq 1/2\). Корректный способ сделать это — представить, что для каждого \(p\in [0,1]\) у нас есть вероятностная мера \(\mathbb P_p\) на пространстве траекторий \(\mathbf X \colon \mathbb N\to \mathbb Z\). Затем определим случайную величину \[ \mathcal N_0 \equiv \mathcal N_0(\mathbf X):= |\{ n\in \mathbb N \,:\: S_n=0\}| \in \mathbb N \cup \{+\infty\} \] Это число посещений частицей начала координат. Утверждение 1 также можно записать как \[ \mathbb P(\mathcal N_0 <\infty)=1 \qquad p\neq 1/2 \]
Упражнение 1 Пусть \(p\neq 1/2\). Докажите, что случайная величина \(\mathcal N_0\) имеет геометрическое распределение \(\mathbb P(\mathcal N_0=k)=(1-\theta)^{k-1}\theta\) для \(k \ge 1\) и некоторого \(\theta = \mathbb P(\tau_0=\infty)\in (0,1)\).
Упражнение 2 Геометрическое распределение \(\mathcal N_0\) в Упражнение 1 зависит от параметра \(\theta\), который, в свою очередь, зависит от \(p\), обозначим его \(\theta_p\). (Напомним, что \(p\neq 1/2\)).
- Докажите, что \(\theta_p=\theta_{1-p}\).
- Докажите, что для \(p>1/2\) отображение \(p\mapsto \theta_p\) является строго возрастающим. (Подсказка: нарисуйте два случайных блуждания, соответствующие \(p>q>1/2\). Если первый шаг равен \(-1\), оба вернутся в \(0\). Если первый шаг равен \(+1\), можете ли вы реализовать их одновременно так, чтобы блуждание с параметром \(p\) никогда не было меньше блуждания с параметром \(q\)?).
Симметричный случай: достоверное возвращение
Когда блуждание симметрично, дрейф отсутствует. Можно предположить, что частица всё же может случайно уйти. Однако оказывается, что возвращение в начало координат почти достоверно. Мощный способ убедиться в этом — проанализировать математическое ожидание числа возвращений.
Для \(\tau_0^{(0)} :=0\) определим для \(n\ge 1\) \[ \tau_0^{(n)}\equiv \tau_0^{(n)}(\mathbf X):= \inf \{m > \tau_0^{(n-1)} \,:\: S_m=0\} \] так что \(\tau_0 \equiv \tau_0^{(1)}\), см. Уравнение 2. \(\tau_0^{(n)}\) — это \(n\)-й момент времени, когда блуждание касается начала координат. Имеет место простой факт \[ \mathbb P(\tau_0^{(n)}<\infty)= \mathbb P(\tau_0<\infty)^n \] поскольку действительно каждый раз, когда мы посещаем \(0\), процесс начинается заново. Таким образом, вероятность того, что мы вернёмся \(n\) раз, в точности равна вероятности того, что мы вернёмся один раз, в степени \(n\). Это даёт нам мощный инструмент для доказательства того, что \(\mathbb P(\tau_0<\infty)=1\). Действительно \[ \begin{aligned} & \sum_{m=0}^\infty \mathbb P(S_m=0)= \mathbb E\left[ \sum_{m=0}^\infty1_{S_m=0} \right]= \mathbb E\left[\sum_{n=0}^\infty 1_{\tau_0^{(n)}<\infty} \right] \\ & = \sum_{n=0}^\infty \mathbb P( \tau_0<\infty)^n = \frac{1}{1- \mathbb P( \tau_0<\infty)} \end{aligned} \]
То есть (обе части могут быть равны \(+\infty\)) \[ \mathbb E[\mathcal N_0]=\sum_{m=0}^\infty \mathbb P(S_m=0) = \frac{1}{1- \mathbb P( \tau_0<\infty)} \tag{3}\]
Утверждение 2 Если \(p = 1/2\), одномерное симметричное случайное блуждание является возвратным, т.е. \(\mathbb P(\tau_0 < \infty) = 1\).
Стоит напомнить оценки Стирлинга для факториала \[ n^n e^{-n} \sqrt{2\pi n} e^{1/(12 n+1)} \le n! \le n^n e^{-n} \sqrt{2\pi n} e^{1/ (12 n)} \qquad n\ge 1 \tag{4}\]
Доказательство (Утверждение 2). Чтобы частица находилась в начале координат в момент времени \(n\), она должна была сделать одинаковое количество шагов вверх и вниз. Это возможно только если \(n\) чётно. Пусть \(n=2k\) для некоторого \(k\ge 1\). Число путей длиной \(2k\) равно \(2^{2k}\). Число путей с ровно \(k\) шагами вверх и \(k\) шагами вниз даётся биномиальным коэффициентом \(\binom{2k}{k}\). Таким образом, вероятность нахождения в начале координат в момент времени \(2k\) равна \[ \mathbb P(S_{2k}=0) = \binom{2k}{k} \left(\frac{1}{2}\right)^{2k} \] Если мы используем приближение Стирлинга (Уравнение 4) для факториалов в последней формуле, мы получаем для \(k\ge 1\) \[ \mathbb P(S_{2k}=0) = \frac{1}{\sqrt{\pi k}} (1-\varepsilon_k), \qquad \frac{1}{8k+3}\le \varepsilon_k\le \frac{1}{8k} \tag{5}\] Поскольку ряд \(\sum_k \mathbb P(S_{2k}=0)\) расходится, мы получаем утверждение теоремы благодаря Уравнение 3.
Доказательство (Другое доказательство Утверждение 2). Пусть \(p_x\) — вероятность того, что блуждающий, стартующий из точки \(x\), когда-нибудь достигнет \(0\). Мы хотим показать, что \(p_x=1\) для всех \(x \in \mathbb Z\). Очевидно, \(p_0=1\). Для \(x \neq 0\), обусловливая по первому шагу, мы имеем: \[ p_x = \frac{1}{2} p_{x-1} + \frac{1}{2} p_{x+1}, \qquad x\in \mathbb Z \setminus \{0\} \] Это уравнение означает, что точки \((x-1, p_{x-1})\), \((x, p_x)\) и \((x+1, p_{x+1})\) коллинеарны. Единственная прямая, проходящая через \((0,1)\) и остающаяся ограниченной (\(0\le p_x \le 1\)) для всех \(x\), — это постоянная прямая \(p_x=1\). Таким образом, блуждание является возвратным.
Упражнение 3 Используйте тот же подход, чтобы доказать, что для \(p\neq 1/2\), \(1-\theta_p=\mathbb P(\tau_0<\infty)<1\). Выразите \(\theta_p\) через ряд.
Примечание 1. Возвратность не является тривиальным следствием симметрии. Если бы мы рассматривали симметричное блуждание на \(\mathbb Z^3\) (и вообще на любой конечно порождённой группе, которая не является виртуально изоморфной \(\mathbb Z\) или \(\mathbb Z^2\)), блуждание было бы невозвратным несмотря на симметрию. Неформально говоря, возвратность является следствием симметрии и того факта, что \(\mathbb Z\) — это маленький граф.
Экскурсии
Статистические свойства так называемых экскурсий оказываются довольно интересными. Здесь мы даём краткий обзор закона времени возвращения.
Определение 2 (Экскурсия) Отрезок пути \((S_m, S_{m+1}, \ldots, S_{m+n})\) является экскурсией из 0 длиной \(n\), если \(S_m=0\), \(S_{m+n}=0\) и \(S_{m+k} \neq 0\) для всех \(k \in \{1, \ldots, n-1\}\). Как только частица касается \(0\), процесс начинается заново, статистические свойства всех экскурсий идентичны. Поэтому мы можем сосредоточиться на первой экскурсии, продолжительность которой задаётся временем первого возвращения \(\tau_0\).
Наша цель — вычислить распределение вероятностей длины экскурсии, т.е. \(\mathbb P(\tau_0 = n)\). Заметим, что если \(S_n=0\), то \(n\) должно быть чётным, поэтому нам нужно вычислить только \(\mathbb P(\tau_0=2k)\) для \(k\ge 1\). Если блуждание несимметрично, такая длина имеет ненулевую вероятность быть бесконечной.
Упражнение 4 Для \(|s|<1\) определим \[ v(x,s):= \mathbb E_x[s^{\tau_0}] = \sum_{k=0}^\infty \mathbb P_x(\tau_0=k)s^k \] где \(\mathbb E_x\) означает математическое ожидание для случайного блуждания, начинающегося в точке \(x\) (это то же самое, что начинаться в \(0\) и достигать точки \(-x\)).
- Докажите, что \(v(x,s)= v(1,s)^x\) для \(x\ge 1\), и \(v(x,s)=v(-1,s)^{-x}\) для \(x\le -1\). Подсказка: стартуя в \(x=2\), нам сначала нужно достичь \(1\), а затем из \(1\) — достичь \(0\).
- Используйте предыдущий факт, чтобы вычислить \(v(x,s)\) для всех \(x,s\), включая \(x=0\). В частности, проверьте \[ v(0,s)=1-\sqrt{1-4 p(1-p)s^2}, \qquad v(1,s)=v(0,s)/(2 s p), \qquad v(-1,s)=v(0,s)/(2s (1-p)) \]
- Выведите, что \(\theta_p=\mathbb P_0(\tau_0=\infty)= |1-2p|\), что, в частности, доказывает результаты предыдущего раздела.
- Используйте формулу Тейлора \[ 1- \sqrt{1-4t}= \sum_{n=1}^\infty A_n t^n, \qquad A_n=\frac{(2n)!}{(2n-1)(n!)^2} \] чтобы вывести, что \[ \mathbb P_0(\tau_0=2k)=A_k p^k (1-p)^k \tag{6}\]
Можно привести и чисто комбинаторное доказательство того же факта.
Лемма 1 (Принцип отражения) Пусть \(S_n\) — симметричное случайное блуждание. Для любых целых чисел \(a>b>0\) количество путей из начала координат в точку \((n,b)\), которые касаются или пересекают уровень \(a\), равно количеству путей из начала координат в точку \((n, 2a-b)\).
Доказательство (Лемма 1). Пусть путь \((S_0, S_1, \ldots, S_n)\) начинается в \(S_0=0\) и заканчивается в \(S_n=b\). Предположим, что этот путь касается или пересекает уровень \(a\). Пусть \(k = \inf\{ j \ge 1 : S_j=a \}\) — первый момент времени, когда путь достигает \(a\).
Мы можем создать новый, отражённый путь \((S'_0, \ldots, S'_n)\), устанавливая инволютивную биекцию между путями, пересекающими \(a\) и заканчивающимися в \(b\), и путями, заканчивающимися в \(2a-b\). Определим:
- Для \(j \le k\) пусть \(S'_j = S_j\). Новый путь идентичен старому до первого момента достижения \(a\).
- Для \(j > k\) пусть \(S'_j = a - (S_j - a) = 2a - S_j\). Мы отражаем оставшуюся часть пути относительно прямой \(y=a\).
Исходный путь начинается в \((0,0)\) и заканчивается в \((n,b)\). Новый путь также начинается в \((0,0)\) (поскольку \(k\ge 1\)) и заканчивается в \((n, S'_n) = (n, 2a - S_n) = (n, 2a-b)\).
Упражнение 5 Используйте Лемма 1, чтобы доказать напрямую \(\mathbb P_0(\tau_0=2k)=A_k p^k (1-p)^k\), подсчитывая пути, которые начинаются и заканчиваются в \(0\) впервые после \(2k\) шагов.
Примечание. Используя приближение Стирлинга для Уравнение 6, мы находим, что для \(p=1/2\) \[ \mathbb P(\tau_0=2k) \approx \frac{1}{2\sqrt{\pi}} k^{-3/2} (1+o_k(1)) \] Следовательно, \(\mathbb E[\tau_0]= \sum_k 2k \mathbb P(\tau_0=2k)=\infty\). Это означает, что, хотя возвращение достоверно, \(\sum_k \mathbb P(\tau_0=2k)=1\), математическое ожидание времени первого возвращения бесконечно.
Упражнение 6 (Пути в положительной полуплоскости) Для симметричного блуждания найдите количество путей из \((0,0)\) в точку \((n,y)\) (с \(y>0\)), которые остаются строго положительными для всех времён \(k \in \{1, \ldots, n\}\).
Путь должен начинаться с шага в \((1,1)\). Затем он должен пройти из \((1,1)\) в \((n,y)\) за \(n-1\) шагов, не касаясь уровня \(y=0\). Общее число путей из \((1,1)\) в \((n,y)\) равно \(N((1,1)\to(n,y))\). По принципу отражения (Лемма 1 с \(a=1\)), число путей, касающихся уровня \(0\), равно числу путей из \((1,-1)\) в \((n,y)\), т.е. \(N((1,-1)\to(n,y))\). Таким образом, искомое число путей равно: \[ N_{>0} = N((1,1)\to(n,y)) - N((1,-1)\to(n,y)) \] Используя формулу \(N((s,a)\to(t,b)) = \binom{t-s}{(b-a+t-s)/2}\), получаем: \[ N_{>0} = \binom{n-1}{(y-1+n-1)/2} - \binom{n-1}{(y-(-1)+n-1)/2} = \frac{y}{n} \binom{n}{(n+y)/2} = \frac{y}{n} N((0,0)\to(n,y)) \]
Упражнение 7 (Максимум в конечной точке) Найдите количество путей из \((0,0)\) в \((n,y)\) таких, что \(S_k < y\) для всех \(k \in \{0, \ldots, n-1\}\).
Эта задача симметрична предыдущей. Рассмотрим обратный путь от \((n,y)\) до \((0,0)\). Это путь длины \(n\), идущий из \((0,0)\) в \((n,-y)\). Условие \(S_k < y\) для исходного пути эквивалентно тому, что для нового пути \(S'_k > -y\) для \(k \in \{1, \ldots, n\}\). Поменяв знак, это то же самое, что и количество путей из \((0,0)\) в \((n,y)\), которые остаются строго положительными. Таким образом, ответ такой же, как и в Упражнение 6: \(\frac{y}{n} N((0,0)\to(n,y))\).
Упражнение 8 (Пути Дика) Найдите количество путей симметричного случайного блуждания из \((0,0)\) в \((2n,0)\), которые остаются неотрицательными, т.е. \(S_k \ge 0\) для всех \(k \in \{0, \ldots, 2n\}\).
Это классическая задача о путях Дика. Ответ — \(n\)-е число Каталана \(C_n\). \[ C_n = \frac{1}{n+1} \binom{2n}{n} \] Это можно вывести с помощью принципа отражения. Общее число путей из \((0,0)\) в \((2n,0)\) равно \(\binom{2n}{n}\). Число «плохих» путей (опускающихся ниже оси) — это число путей, которые касаются или пересекают прямую \(y=-1\). По принципу отражения, это равно числу путей из \((0,0)\) в \((2n,-2)\), что составляет \(\binom{2n}{n-1}\). Число «хороших» путей — это разность: \[ \binom{2n}{n} - \binom{2n}{n-1} = \frac{1}{n+1}\binom{2n}{n} \]
Упражнение 9 (Мосты) Найдите количество путей симметричного случайного блуждания из \((0,0)\) в \((2n,0)\) со строго положительными внутренними вершинами, т.е. \(S_k > 0\) для \(k \in \{1, \ldots, 2n-1\}\).
Такой путь должен начинаться с шага в \((1,1)\) и заканчиваться шагом из \((2n-1,1)\). Часть пути от \((1,1)\) до \((2n-1,1)\) имеет длину \(2n-2\) и не должна опускаться ниже уровня \(y=1\). Это эквивалентно неотрицательному пути длины \(2n-2\) из \((0,0)\) в \((0,0)\). Согласно Упражнение 8 (с заменой \(n\) на \(n-1\)), это число равно \((n-1)\)-му числу Каталана: \[ C_{n-1} = \frac{1}{n} \binom{2n-2}{n-1} \]
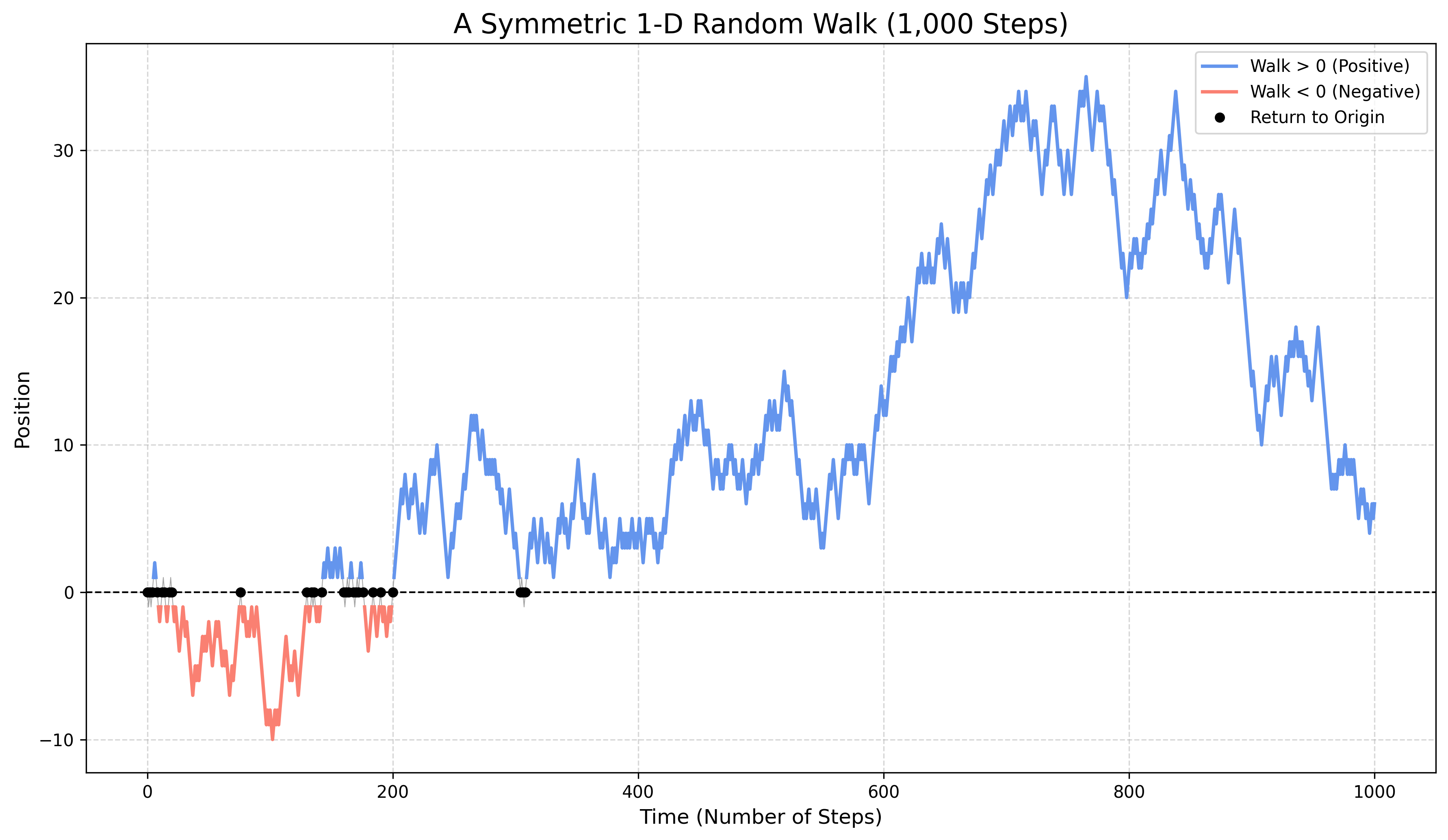
Закон арксинуса
Удивительный результат касается времени, которое симметричное случайное блуждание проводит по одну сторону от оси. Оказывается, наиболее вероятные сценарии — это когда частица проводит почти всё своё время на положительной стороне или почти всё своё время на отрицательной стороне. Это количественно описывается законом арксинуса. Далее мы предполагаем, что \(p=1/2\).
Чтобы точно сформулировать результат, нам нужно подходящее определение времени, проведённого на положительной стороне. Пусть \(\pi_{2n}\) — это число отрезков пути \((S_0, S_1, \ldots, S_{2n})\), которые лежат на или выше горизонтальной оси. То есть, \[ \pi_{2n} := |\{k \in \{1, \ldots, 2n\} : S_{k-1} \ge 0 \text{ and } S_k \ge 0 \}| \] Заметим, что поскольку \(S_k\) может изменяться только на \(\pm 1\) на каждом шаге, путь не может пересечь ось с \(S_{k-1} > 0\) до \(S_k < 0\) (или наоборот) за один шаг, не пройдя через 0. Это означает, что \(\pi_{2n}\) должно быть чётным целым числом.
Мы также определяем \[ L_{2n} = \max\{m \le 2n : S_m=0\} \] как время последнего посещения начала координат до момента времени \(2n\).
Теорема 1 (Закон арксинуса Леви) Пусть \((S_n)_{n\ge 0}\) — симметричное одномерное случайное блуждание, а \(\pi_{2n}\) — число отрезков на или выше оси, как определено выше. Доля времени \(\pi_{2n}/(2n)\) сходится по распределению к распределению арксинуса на \([0,1]\): \[ \lim_{n\to\infty} \mathbb P\left( \frac{\pi_{2n}}{2n} \le x \right) = \frac{2}{\pi} \arcsin(\sqrt{x}) \] для любого \(x\in[0,1]\).
Более того, \(L_{2n}\) имеет то же распределение, что и \(\pi_{2n}\), и, таким образом, тот же результат справедлив для \(L_{2n}\)
Плотность распределения арксинуса, \(\varrho(x) = (\pi\sqrt{x(1-x)})^{-1}\), имеет U-образную форму, что подтверждает, что частица, скорее всего, проводит своё время либо на положительной, либо на отрицательной стороне оси.
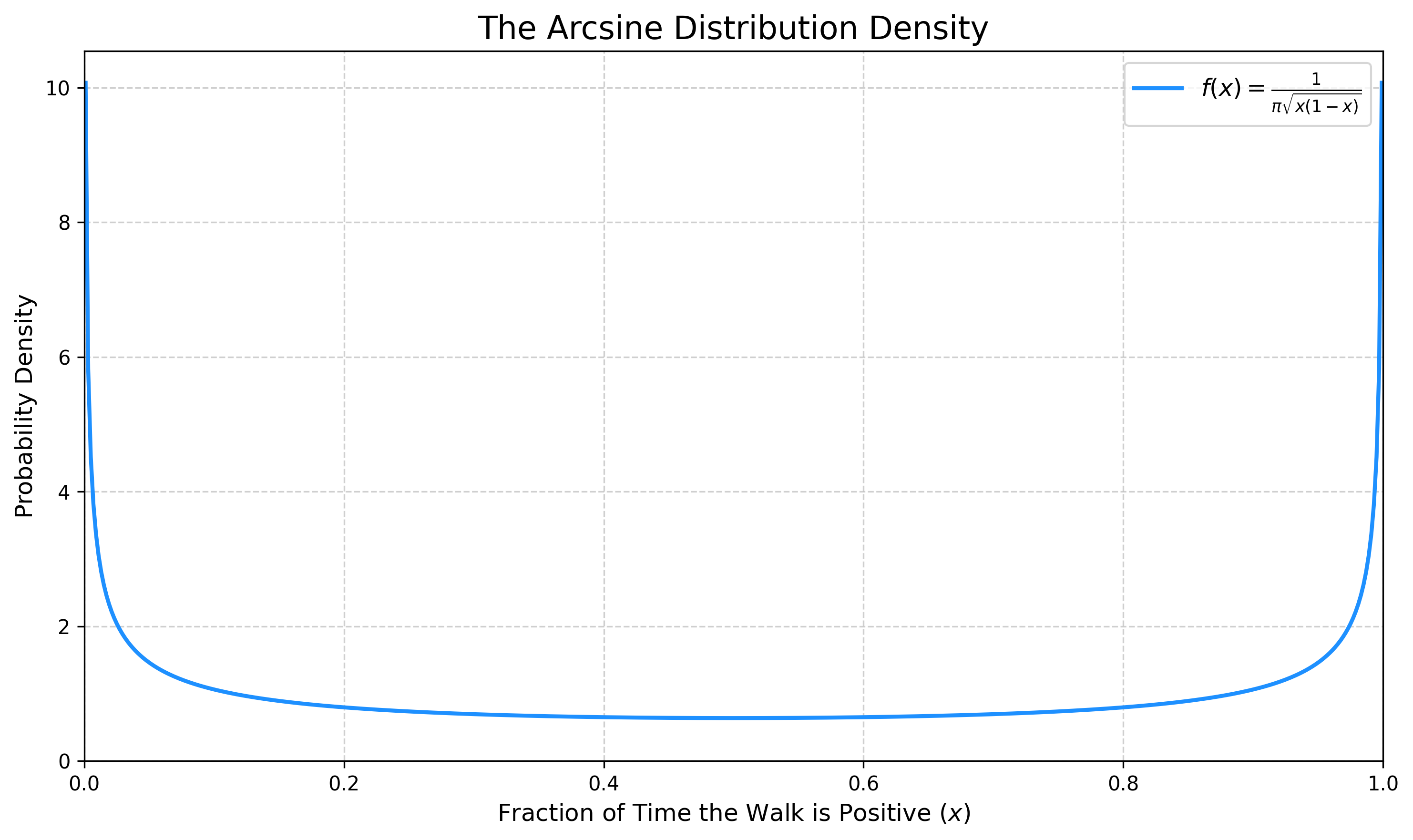
Основная идея доказательства состоит в том, чтобы найти точное выражение для \(\mathbb P(\pi_{2n}=2k)\) при конечном \(n\), а затем использовать приближение Стирлинга для нахождения предела. Для ясности обозначим через \(N\big((s,a)\to (t,b))\) число путей, идущих из точки \(a\) в момент времени (число шагов) \(s\) в точку \(b\) в момент времени \(t\). Это \[ N\big((s,a)\to (t,b))= \binom{t-s}{(b-a +t-s)/2} \] что означает \(0\), если \((b-a +t-s)\) нечётно.
Лемма 2 Тогда \[ \mathbb P(L_{2n}=2k) = u_{2k} u_{2(n-k)} \tag{7}\] где \(u_{2m}\) — это вероятность нахождения в \(0\) после \(2m\) шагов, \(u_{2m}=\binom{2m}{m} 4^{-m}\).
Доказательство (Лемма 2). Начнём со случая \(k=n\), то есть покажем, что \(\mathbb P(\tau_0 > 2n) = u_{2n}\). Путь не возвращается в \(0\) тогда и только тогда, когда он остаётся строго на положительной стороне или строго на отрицательной стороне. В силу симметрии эти две вероятности равны. Вычислим вероятность оставаться строго положительным, \(P(S_1 > 0, \ldots, S_{2n} > 0)\), то есть \(S_1=1\) и последующие \(2n-1\) шагов, начиная с \(1\), никогда не достигают \(0\).
Число таких путей можно найти с помощью принципа отражения (Лемма 1). Общее число путей из \((1,1)\), которые остаются строго выше \(0\) в течение \(2n-1\) шагов, даётся результатом следующей телескопической суммы по всем возможным конечным положениям \(2r > 0\): \[ \begin{aligned} & \sum_{r=1}^\infty \left[ N\big((1,1)\to(2n,2r)\big) - N\big((1,-1)\to(2n,2r)\big) \right] \\ & = \sum_{r=1}^\infty \left[ N\big((0,0)\to(2n-1,2r-1)\big) - N \big((0,0)\to(2n-1,2r+1)\big) \right] = \\ & N \big((0,0)\to(2n-1,1)\big) =\binom{2n-1}{n} \end{aligned} \]
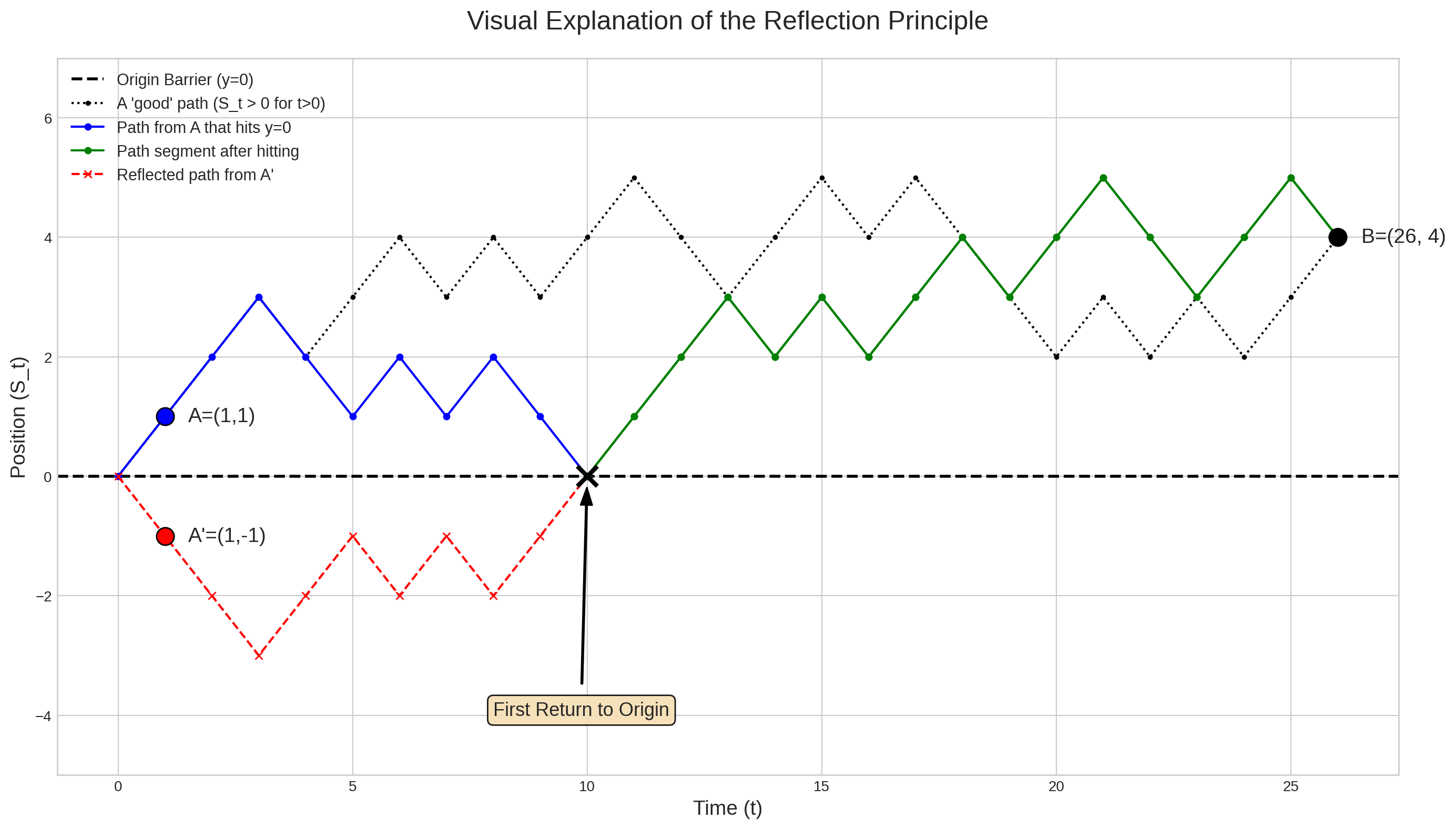
Для симметричного блуждания все пути имеют одинаковую вероятность. Так мы можем найти вероятность невозвращения в начало координат: \[ \mathbb P(\tau_0 > 2n) =2 \mathbb P(S_1=1, S_2 \ge 1,\ldots S_{2n}\ge 1) = 2 \binom{2n-1}{n} 2^{-2n} = u_{2n} \]
Теперь рассмотрим общий случай \(k\le n\). Событие \(\{L_{2n}=2k\}\) означает, что блуждание находится в начале координат в момент времени \(2k\) и не возвращается в начало координат между моментами времени \(2k+1\) и \(2n\). Мы можем записать это как: \[ \mathbb P(L_{2n}=2k) = \mathbb P(S_{2k}=0 \text{ and } S_j \neq 0 \text{ for } 2k < j \le 2n) \] Но событие \(\{S_{2k}=0\}\) не зависит от последующего пути: \[ \mathbb P(L_{2n}=2k) = \mathbb P(S_{2k}=0) \, \mathbb P(\tau'_0 > 2n-2k) \] где \(\tau'_0\) — это время первого возвращения для нового блуждания, начинающегося в \(0\) в момент времени \(2k\). Используя результат для \(k=n\), это становится: \[ \mathbb P(L_{2n}=2k) = u_{2k} u_{2(n-k)} \]
Упражнение 10 Определим \(\alpha_{2k,2n}=\mathbb P(\pi_{2n}=2k)\). Мы хотим доказать, что \(\alpha_{2k,2n}=u_{2k} u_{2(n-k)}\). Пусть \(f_{2m}=\mathbb P(\tau_0=2m)\).
а) Докажите, что \(\alpha_{2k,2}= u_{2k} u_{2-2k}\) для \(k=0,1\). б) Докажите, что \(\alpha_{2n,2n}=u_{2n}\). в) Проведите индукцию по \(n\), чтобы проверить, что для \(k=1,\ldots,n-1\) \[ \alpha_{2k,2n}=\tfrac 12 u_{2n-2k}\sum_{m=1}^k f_{2m} u_{2k-2m} + \tfrac 12 u_{2k}\sum_{m=1}^{n-k} f_{2m} u_{2n -2k-2m} \] г) Обусловливая по времени первого возвращения, проверьте, что \(u_{2k}=\sum_{m=1}^k f_{2m} u_{2(k-m)}\). д) Используйте пункты в) и г), чтобы сделать вывод.
Из Лемма 2 и Упражнение 10 мы получили: \[ \mathbb P(\pi_{2n}=2k) = \mathbb P(L_{2n}=2k)= u_{2k} u_{2(n-k)} = \binom{2k}{k} \binom{2(n-k)}{n-k} 4^{-n} \tag{8}\] Теперь мы можем доказать теорему.
Доказательство (Теорема 1). Нас интересует интегральная функция распределения доли времени \(\frac{\pi_{2n}}{2n}\). Пусть \(x \in (0,1)\), тогда \[ \mathbb P\left( \frac{\pi_{2n}}{2n} \le x \right) = \sum_{j=0}^{\lfloor nx \rfloor} \mathbb P(\pi_{2n}=2j) = \int_0^{\lfloor nx \rfloor/n} \varrho_n(y) dy \tag{9}\] где \[ \varrho_n(y):= n \mathbb P(\pi_{2n}=2j) \qquad \text{for $j/n \le y \le (j+1)/n $} \] По Уравнение 5 и Уравнение 8 \[ n \mathbb P(\pi_{2n}=2j)=n u_{2j} u_{2(n-j)}= \frac{1}{\sqrt{\pi j/n}} \frac{1}{\sqrt{\pi(1-j/n)}} (1-\varepsilon_j) (1-\varepsilon_{n-j}) \] и мы сразу видим, что \(\varrho_{n}(x)\to \varrho(x)= (\pi\sqrt{x(1-x)})^{-1}\) равномерно на компактах в \((0,1)\). Таким образом, переходя к пределу \(n\to \infty\) в Уравнение 9, мы получаем утверждение теоремы.
Равенство распределений \(\pi_{2n}\) и \(L_{2n}\) показано в Уравнение 8.
Многомерное случайное блуждание
Естественным обобщением является случайное блуждание на \(l\)-мерной целочисленной решётке \(\mathbb{Z}^l\). Блуждающий начинает в точке \(\mathbf{x} \in \mathbb{Z}^l\), \(\mathbf{S}_0 = \mathbf{x}\). На каждом шаге он перемещается в одну из \(2l\) соседних точек с равной вероятностью \(1/(2l)\). То есть, \(\mathbf{S}_n = \mathbf{x} + \sum_{i=1}^n \mathbf{X}_i\), где \(\mathbf{X}_i\) — независимые случайные векторы, принимающие значения \(\pm \mathbf{e}_j\) (где \(\mathbf{e}_j\) — стандартные базисные векторы) с вероятностью \(1/(2l)\).
Как и в одномерном случае, мы можем спросить, является ли блуждание возвратным (возвращается в начало координат с вероятностью 1) или невозвратным. Ответ, как оказывается, зависит от размерности \(l\).
Характеристическая функция и вероятности перехода
Для анализа многомерного случая удобно использовать характеристические функции. Пусть \(\mathbb{P}_{\mathbf{x}}(\mathbf{S}_n = \mathbf{y})\) — вероятность того, что блуждание, начавшееся в \(\mathbf{x}\), окажется в точке \(\mathbf{y}\) через \(n\) шагов. Характеристическая функция случайного вектора \(\mathbf{S}_n\) (при условии старта из \(\mathbf{x}\)) определяется как: \[ F(\mathbf{\theta}, n, \mathbf{x}) = \mathbb{E}_{\mathbf{x}}[e^{i \mathbf{\theta} \cdot \mathbf{S}_n}] = \sum_{\mathbf{y} \in \mathbb{Z}^l} \mathbb{P}_{\mathbf{x}}(\mathbf{S}_n = \mathbf{y}) e^{i \mathbf{\theta} \cdot \mathbf{y}} \] где \(\mathbf{\theta} = (\theta_1, \ldots, \theta_l) \in \mathbb{T}^l \simeq (-\pi, \pi]^l\). Благодаря независимости шагов, мы имеем: \[ F(\mathbf{\theta}, n, \mathbf{x}) = e^{i \mathbf{\theta} \cdot \mathbf{x}} \left( \mathbb{E}[e^{i \mathbf{\theta} \cdot \mathbf{X}_1}] \right)^n \] Математическое ожидание для одного шага: \[ \mathbb{E}[e^{i \mathbf{\theta} \cdot \mathbf{X}_1}] = \sum_{j=1}^l \frac{1}{2l} (e^{i\theta_j} + e^{-i\theta_j}) = \frac{1}{l} \sum_{j=1}^l \cos(\theta_j) =: \Phi(\mathbf{\theta}) \] Таким образом, \(F(\mathbf{\theta}, n, \mathbf{x}) = e^{i \mathbf{\theta} \cdot \mathbf{x}} [\Phi(\mathbf{\theta})]^n\). Вероятности перехода можно восстановить с помощью обратного преобразования Фурье: \[ \mathbb{P}_{\mathbf{x}}(\mathbf{S}_n = \mathbf{y}) = \frac{1}{(2\pi)^l} \int_{(-\pi, \pi]^l} F(\mathbf{\theta}, n, \mathbf{x}) e^{-i \mathbf{\theta} \cdot \mathbf{y}} d\mathbf{\theta} = \frac{1}{(2\pi)^l} \int_{(-\pi, \pi]^l} e^{i \mathbf{\theta} \cdot (\mathbf{x}-\mathbf{y})} [\Phi(\mathbf{\theta})]^n d\mathbf{\theta} \tag{10}\]
Критерий Пойа: возвратность и невозвратность
Мы видели в Упражнение 1 (что легко переносится на любую размерность), что если блуждание невозвратно, то число возвращений в \(0\) является геометрической случайной величиной, следовательно, имеет конечное математическое ожидание. Поэтому блуждание возвратно тогда и только тогда, когда математическое ожидание числа возвращений в начало координат бесконечно. Обозначим это математическое ожидание как \(g(\mathbf{0}, \mathbf{0}) = \sum_{n=0}^\infty \mathbb{P}_{\mathbf{0}}(\mathbf{S}_n = \mathbf{0})\). Используя Уравнение 10, поскольку \(|\Phi(\mathbf{\theta})| < 1\) за исключением двух точек (\(\theta_1=\ldots=\theta_l=0\) и \(\theta_1=\ldots=\theta_l=\pi\)):
\[ g(\mathbf{0}, \mathbf{0}) = \sum_{n=0}^\infty \frac{1}{(2\pi)^l} \int_{(-\pi, \pi]^l} [\Phi(\mathbf{\theta})]^n d\mathbf{\theta} = \frac{1}{(2\pi)^l} \int_{(-\pi, \pi]^l} \sum_{n=0}^\infty [\Phi(\mathbf{\theta})]^n d\mathbf{\theta} = \frac{1}{(2\pi)^l} \int_{(-\pi, \pi]^l} \frac{1}{1 - \Phi(\mathbf{\theta})} d\mathbf{\theta} \]
Блуждание возвратно, если этот интеграл расходится, и невозвратно, если он сходится. Сходимость определяется поведением подынтегральной функции вблизи точек, где знаменатель обращается в ноль, т.е. \(\mathbf{\theta} \approx \mathbf{0}\). Вблизи нуля, \(\cos(\theta_j) \approx 1 - \theta_j^2/2\), поэтому: \[ 1 - \Phi(\mathbf{\theta}) = 1 - \frac{1}{l} \sum_{j=1}^l \cos(\theta_j) \approx 1 - \frac{1}{l} \sum_{j=1}^l (1 - \theta_j^2/2) = \frac{1}{2l} \sum_{j=1}^l \theta_j^2 = \frac{\|\mathbf{\theta}\|^2}{2l} \] Таким образом, сходимость интеграла зависит от сходимости \(\int \frac{d\mathbf{\theta}}{\|\mathbf{\theta}\|^2}\) в окрестности нуля. В полярных координатах \(d\mathbf{\theta} \sim r^{l-1}dr\), поэтому интеграл ведёт себя как \(\int_0 \frac{r^{l-1}}{r^2} dr = \int_0 r^{l-3} dr\).
- При \(l=1\), интеграл \(\int r^{-2}dr\) расходится. Блуждание возвратно.
- При \(l=2\), интеграл \(\int r^{-1}dr\) расходится. Блуждание возвратно.
- При \(l \ge 3\), показатель степени \(l-3 \ge 0 > -1\), поэтому интеграл сходится. Блуждание невозвратно.
Этот результат известен как теорема Пойа: симметричное случайное блуждание на \(\mathbb{Z}^l\) возвратно для \(l=1,2\) и невозвратно для \(l \ge 3\). Это частный случай результата, изложенного в Remark 1.
Моделирование блуждания
Мы можем легко проверить различные утверждения численно, поскольку сходимость происходит довольно быстро.
Первый возврат к \(0\)
Сначала мы явно вычислили закон первого возвращения в \(0\). Его математическое ожидание бесконечно, поэтому при моделировании нужно быть осторожным и обрезать симуляции на определённом количестве шагов. Это вносит смещение, о котором мы сообщаем, но не компенсируем его здесь.
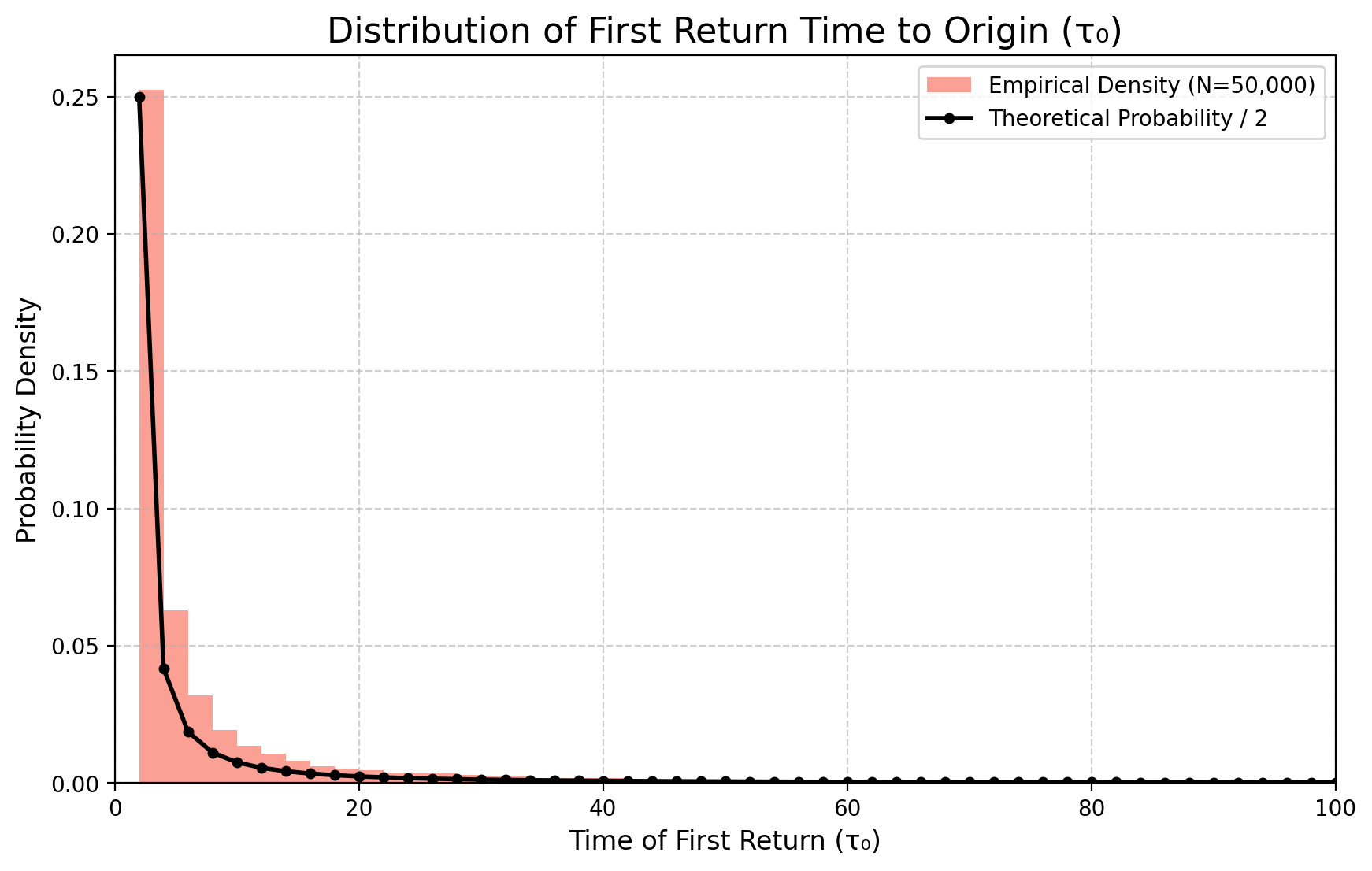
Распределение арксинуса
Затем мы моделируем методом Монте-Карло количество времени, которое случайное блуждание остаётся положительным.
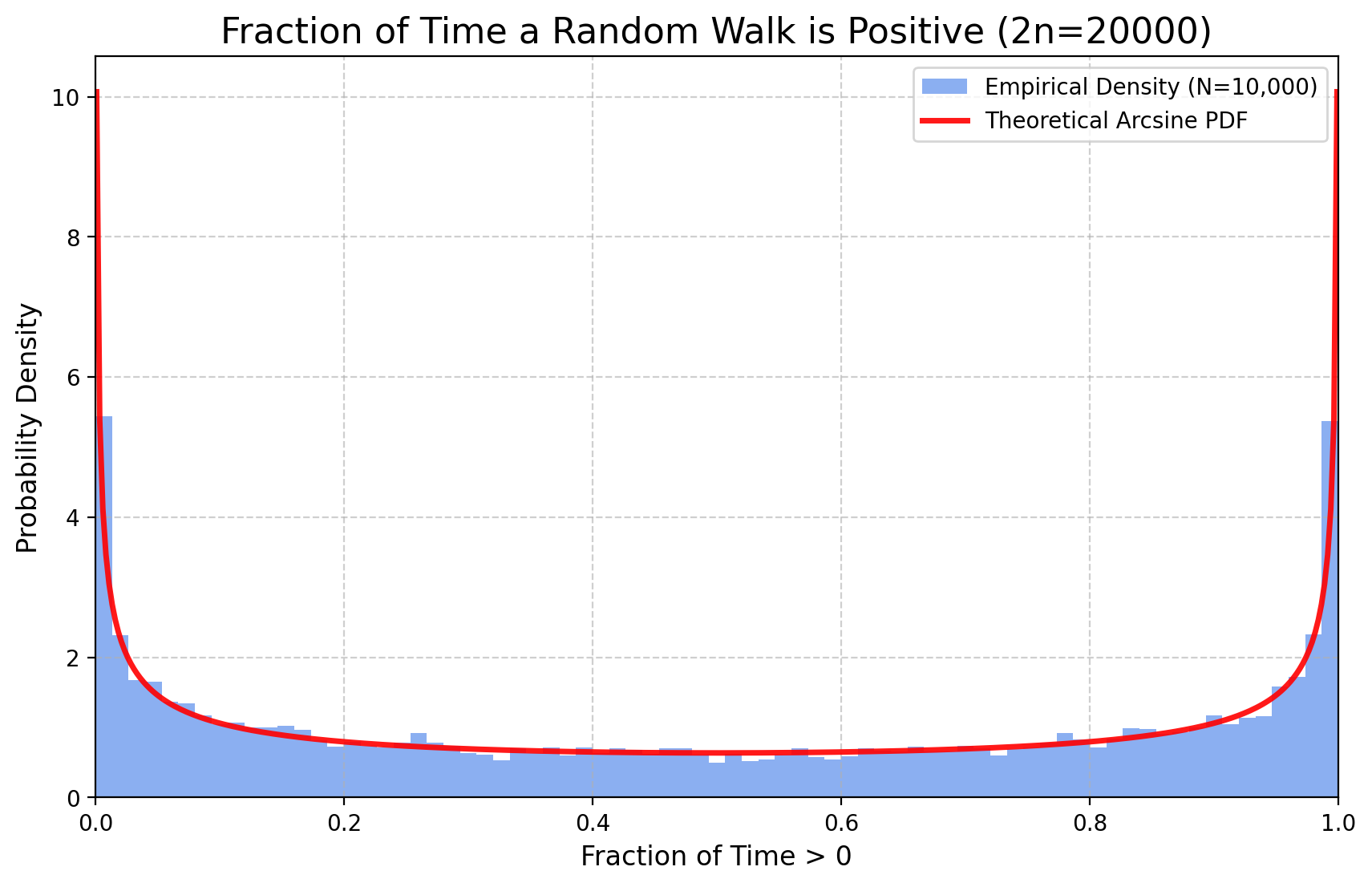
Грубо говоря, эти распределения универсальны, то есть они представляют собой скейлинговый предел для нескольких различных случайных динамик. Например, мы можем изменить закон \(X_i\) на любое центрированное распределение с конечной дисперсией (скажем, \(1\)), чтобы сойтись к тому же закону.
На этом графике используется непрерывное равномерное распределение.
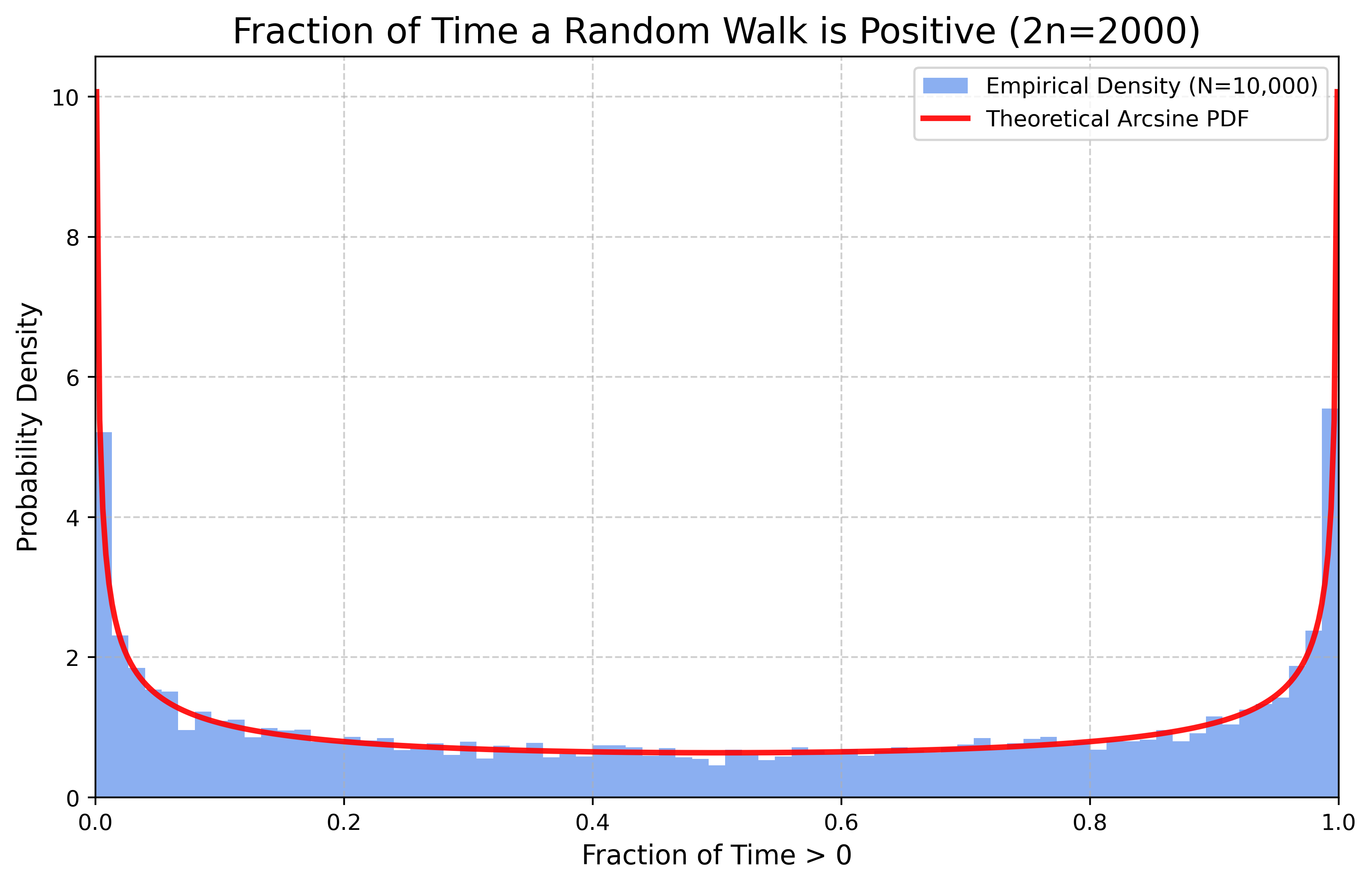
Вы можете попробовать проверить универсальность распределения арксинуса. Вы можете посмотреть, что происходит с различными распределениями. Если распределения несимметричны (например, центрированное показательное \(X-\mathbb E[X]\) с показательным \(X\)), чего вы ожидаете?
#| '!! shinylive warning !!': |
#| shinylive does not work in self-contained HTML documents.
#| Please set `embed-resources: false` in your metadata.
#| standalone: true
#| components: [editor, viewer]
#| viewerHeight: 1080
#| editorHeight: 240
#| layout: vertical
# ========= 1. IMPORTS & CONFIGURATION =========
from shiny import App, render, ui, reactive, req
import numpy as np
import matplotlib.pyplot as plt
# Configuration dictionary for UI inputs
ARCSIN_CONFIG = {
'n_slider': {
'min': 10, 'max': 2000, 'value': 200, 'step': 2,
},
'N_samples_slider': {
'min': 100, 'max': 10000, 'value': 5000, 'step': 100,
},
'distribution': {
'choices': ['Symmetric {-1, +1}', 'Standard Normal N(0,1)', 'Uniform [-1, 1]', 'Centered Exponential'],
'selected': 'Symmetric {-1, +1}',
},
'filename': {'value': 'arcsin_simulation.png'},
}
# ========= 2. UI DEFINITION =========
app_ui = ui.page_sidebar(
ui.sidebar(
ui.h3("Arcsine Law Simulation"),
ui.p("This simulation shows the distribution of the fraction of time a 1-D random walk spends on the positive side."),
ui.hr(),
ui.input_slider("n", "Number of Steps (2n):", **ARCSIN_CONFIG['n_slider']),
ui.input_slider("N_samples", "Number of Walks (N):", **ARCSIN_CONFIG['N_samples_slider']),
ui.input_select("distribution", "Step Distribution:", **ARCSIN_CONFIG['distribution']),
ui.hr(),
ui.input_action_button("run_button", "Run Simulation", class_="btn-success w-100"),
ui.hr(),
ui.h4("Saving Options"),
ui.input_checkbox("save_plot", "Save Plot", value=False),
ui.panel_conditional(
"input.save_plot",
ui.input_text("filename", "Filename:", **ARCSIN_CONFIG['filename']),
),
title="Controls",
),
ui.output_plot("arcsin_plot", height="700px"),
title="Arcsine Law for Random Walks",
)
# ========= 3. SERVER LOGIC =========
def server(input, output, session):
figure_to_display = reactive.Value(None)
# --- Helper Functions ---
def generate_steps(dist_name, size):
"""Generates random steps based on the selected distribution."""
if dist_name == 'Symmetric {-1, +1}':
return np.random.choice([-1, 1], size=size)
if dist_name == 'Standard Normal N(0,1)':
return np.random.randn(*size)
if dist_name == 'Uniform [-1, 1]':
return np.random.uniform(-1, 1, size=size)
if dist_name == 'Centered Exponential':
# Asymmetric distribution with mean 0
return np.random.standard_exponential(size=size) - 1
raise ValueError(f"Unknown distribution: {dist_name}")
def get_arcsin_pdf(x):
"""Calculates the PDF of the Arcsine distribution."""
return 1 / (np.pi * np.sqrt(x * (1 - x)))
@reactive.Effect
@reactive.event(input.run_button, ignore_init=True)
def _():
"""Runs the simulation when the action button is clicked."""
n = input.n()
N = input.N_samples()
dist_name = input.distribution()
try:
# --- Perform Simulation ---
steps = generate_steps(dist_name, size=(N, n))
walks = np.cumsum(steps, axis=1)
time_positive = np.sum(walks > 0, axis=1)
fractions = time_positive / n
# --- Create Plot ---
fig, ax = plt.subplots(figsize=(10, 6))
num_bins = min(80, max(20, N // 100))
ax.hist(fractions, bins=num_bins, density=True, alpha=0.75,
label=f'Empirical Density (N={N:,})')
# --- Plot Theoretical PDF (only if applicable) ---
symmetric_dists = ['Symmetric {-1, +1}', 'Standard Normal N(0,1)', 'Uniform [-1, 1]']
if dist_name in symmetric_dists:
x_axis = np.linspace(1e-4, 1 - 1e-4, 500)
ax.plot(x_axis, get_arcsin_pdf(x_axis), 'r-', lw=2.5, alpha=0.9,
label='Theoretical Arcsine PDF')
# --- Customize Plot ---
ax.set_title(f"Fraction of Time Positive (Steps ~ {dist_name}, 2n={n})")
ax.set_xlabel("Fraction of Time > 0")
ax.set_ylabel("Probability Density")
ax.set_xlim(0, 1)
ax.set_ylim(bottom=0)
ax.legend()
ax.grid(True, linestyle='--', alpha=0.6)
# --- Handle Saving ---
if input.save_plot():
req(input.filename(), cancel_output=True)
fig.savefig(input.filename(), dpi=400, bbox_inches='tight')
figure_to_display.set(fig)
plt.close(fig)
except Exception as e:
fig, ax = plt.subplots()
ax.text(0.5, 0.5, f"An error occurred: {e}", ha='center', va='center', wrap=True)
figure_to_display.set(fig)
plt.close(fig)
@output
@render.plot
def arcsin_plot():
"""Renders the plot from the reactive value."""
fig = figure_to_display.get()
req(fig)
return fig
# ========= 4. APP INSTANTIATION =========
app = App(app_ui, server)Повторяемость и кратковременность в многомерном пространстве
Если мы запустим трёхмерное случайное блуждание, скажем, \(X\), и возьмём его проекцию \(Y\) на горизонтальную плоскость, спроецированное блуждание не будет двигаться при вертикальном движении \(X\). Но если мы пропустим этот момент (что не изменит свойства возврата к \(0\) или нет), \(Y\) просто совершит двумерное случайное блуждание. Очевидно, что \(Y\) будет пересекать свой собственный путь (возвращаться туда, где был) гораздо чаще, чем \(X\). Действительно, каждый раз, когда \(X\) возвращается к \(0\), \(Y\) также будет делать это, в то время как обратное неверно (когда \(Y\) находится в начале координат, \(X\) может находиться в некоторой точке \((0,0,z)\)). Это ещё более верно, если мы проецируем только на одну ось координат. Другими словами, очевидно, что чем выше размерность, тем более кратковременным является блуждание (для симметричных случайных блужданий). Этот неформальный аргумент легко превратить в строгое доказательство. В этом видео показано описанное явление.