Центральная предельная теорема
Это краткий обзор центральной предельной теоремы (ЦПТ), целью которого является придать конкретный смысл природе сходимости (по распределению, а не по вероятности).
Эта страница содержит (в конце) интерактивный контент, который вы можете свободно изучать и изменять. Для более сложных изменений рекомендуется запустить и отредактировать интерактивный Jupyter Notebook. Вы можете:
- Запустить его на компьютере с установленным Python/Jupyter-lab (требуются
ipywidgets,numpy,matplotlib). - Запустить его с помощью онлайн-сервиса. Официальный сайт Jupyter предоставляет бесплатный и открытый сервис. Если вам нужна большая вычислительная мощность, вы можете импортировать блокнот в Google Colab (требуется учётная запись Google).
Результаты о сходимости
Рассмотрим некоторые основные результаты о сходимости для сумм центрированных случайных величин с конечной дисперсией.
Классическая формулировка
Теорема 1 (Центральная предельная теорема) Пусть \((X_n)_{n\ge 1}\) — последовательность независимых одинаково распределённых (i.i.d.) вещественнозначных случайных величин с \(\mathbb E[|X_n|^2]<\infty\). Обозначим \(m:= \mathbb E[X_n]\), \(\sigma:= \sqrt{\mathbb{D}[X_n]}\) и \[ S_n:= \frac{1}{\sqrt{n}} \sum_{i=1}^n \frac{X_i -m}{\sigma} \tag{1}\] Тогда \(S_n\) сходится по распределению к стандартной нормальной случайной величине, скажем \(Z\sim \mathcal N(0,1)\). Другими словами, для каждой ограниченной измеримой функции \(f \colon \mathbb R\to \mathbb R\), непрерывной почти всюду, выполняется \[ \lim_{n\to \infty} \mathbb E[f(S_n)] = \frac{1}{\sqrt{2 \pi}} \int f(x) e^{-x^2/2} dx \]
В частности, из предыдущей теоремы можно вывести равномерную сходимость функции распределения \[ \lim_{n\to \infty} \sup_{a<b}\left| \mathbb P( a< S_n \le b) - \mathbb P(a<Z\le b)\right|=0 \]
Количественная версия
Предыдущая Теорема 1 не затрагивает скорость сходимости.
Теорема 2 (Количественная центральная предельная теорема) Пусть \((Y_n)_{n\ge 1}\) — последовательность независимых случайных величин с \(\mathbb E[Y_n]=0\) и \(\mathbb E[Y_n^2]=1\), \(\mathbb E[|Y_n|^3]<\infty\). Пусть \[ S_n:= \frac{1}{\sqrt{n}} \sum_{i=1}^n Y_i \] Для \(g\in C^3_b(\mathbb R)\) с \(C:= \sup_x |g'''(x)|\) выполняется \[ |\mathbb{E}[g(S_n)] - \mathbb{E}[g(Z)]| \le \frac{C}{6\sqrt{n}} \left( \frac{2^{3/2}}{\sqrt{\pi}}+\frac{1}{n}\sum_{k=1}^n \mathbb E[|Y_k|^3] \right) \] где \(Z\sim \mathcal N(0,1)\); а именно \[ \mathbb E[g(Z)] = \tfrac{1}{\sqrt{2 \pi}} \int g(x) e^{-x^2/2} dx \]
Лемма 1 Пусть \(V\), \(Y\) и \(Z\) — три случайные величины, такие что
- \(V\) и \(Y\) независимы; \(V\) и \(Z\) независимы.
- \(Y\) и \(Z\) имеют конечный третий момент.
- \(\mathbb E[Y] = \mathbb E[Z]\) и \(\mathbb E[Y^2] =\mathbb E[Z^2]\).
Тогда для любой \(g \in C_b^3\), полагая \(C := \sup_{x \in \mathbb{R}} |g'''(x)|\), выполняется следующее неравенство: \[ |\mathbb E[g(V +Y )] - \mathbb E[g(V + Z)]| \le \frac{C}{6} \left( \mathbb E[|Y|^3] + \mathbb E[|Z|^3] \right) \]
Доказательство (Лемма 1). По формуле Тейлора, для трёх точек \(v,y,z \in \mathbb R\) выполняется \[ g(v+y)-g(v+z)= g'(v) (y-z) + \tfrac 12 g''(v)(y^2-z^2) + R(v,y)- R(v,z) \] где остаточные члены \(R(v,\cdot)\) ограничены как \(|R(v,x)|\le C |x|^3/6\). Теперь вычислим предыдущую формулу для каждого \(\omega\in \Omega\) в точках \(v=V(\omega)\), \(y=Y(\omega)\) и \(z=Z(\omega)\), и возьмём математическое ожидание. Тогда \(\mathbb E[g'(V) (Y-Z)]=\mathbb E[g'(V)] \mathbb E[(Y-Z)]=0\) (используя гипотезы о независимости и равенстве математических ожиданий). Аналогично для члена \(g''(V)(Y^2-Z^2)\). Таким образом
\[ \left| \mathbb E[g(V+Y)-g(V+Z)] \right| = \left| \mathbb E[R(V,Y) - R(V,Z)] \right| \le \frac{C}{6} \left( \mathbb E[|Y|^3] + \mathbb E[|Z|^3] \right) \]
Лемма 2 Пусть \(g \in C^3_b(\mathbb R)\), пусть \(Y_1,\ldots,Y_n\) — независимые случайные величины, и \(Z_1,\ldots,Z_n\) — другой набор независимых случайных величин. Предположим, что \(\mathbb E[Y_i]=\mathbb E[Z_i]\) и \(\mathbb E[Y_i^2]= \mathbb E[Z_i^2]<\infty\). Пусть \(C\) определено как в Лемма 1. Тогда \[ \left|\mathbb E\left[g\left(\tfrac{Y_1+\ldots+Y_n}{\sqrt{n}}\right) - g\left(\tfrac{Z_1+\ldots+Z_n}{\sqrt{n}}\right) \right] \right| \le \frac{C}{6 n^{3/2}}\sum_{k=1}^{n} \left( \mathbb E[|Y_k|^3] + \mathbb E[|Z_k|^3]\right) \] В частности, если \(Y_i\) являются i.i.d. и \(Z_i\) являются i.i.d. (в общем случае с другим распределением) \[ \left|\mathbb E\left[g\left(\tfrac{Y_1+\ldots+Y_n}{\sqrt{n}}\right) - g\left(\tfrac{Z_1+\ldots+Z_n}{\sqrt{n}}\right) \right] \right| \le \frac{C \left( \mathbb E[|Y_1|^3] + \mathbb E[|Z_1|^3] \right)}{6 \sqrt{n}} \]
Доказательство (Лемма 2). Без ограничения общности, можно предположить, что все \(Y_1,\ldots,Y_n,Z_1,\ldots,Z_n\) являются независимыми случайными величинами. Тогда запишем \(V_k=(Y_1+\ldots +Y_{k-1} + Z_{k+1}+\ldots +Z_{n})/\sqrt{n}\), чтобы получить \[ \begin{aligned} \left| \mathbb E\left[g\left(\tfrac{Y_1+\ldots+Y_n}{\sqrt{n}}\right) - g\left(\tfrac{Z_1+\ldots+Z_n}{\sqrt{n}}\right) \right] \right| & = \left| \sum_{k=1}^{n} \mathbb E\left[g\left(V_k + \tfrac{Y_{k}}{\sqrt{n}}\right) - g\left(V_k+\tfrac{Z_{k}}{\sqrt{n}}\right) \right] \right| \\ & \le \sum_{k=1}^{n} \frac{C}6 \left( \mathbb E[|Y_k/\sqrt{n}|^3] + \mathbb E[|Z_k/\sqrt{n}|^3]\right) \end{aligned} \] где в последнем неравенстве мы использовали Лемма 1 \(n\) раз.
Доказательство (Теорема 2). Если \(Z_i\) являются i.i.d. стандартными нормальными, то \((Z_1+\ldots + Z_n)/\sqrt{n}\) также является стандартной нормальной величиной, и, следовательно, её распределение не зависит от \(n\). Теорема 2, таким образом, является следствием Лемма 2 и тождества \(\mathbb E[|Z_i|^3]=2^{3/2}/\sqrt{\pi}\).
Упражнение 1 Пусть \(Z\sim \mathcal N(0,1)\) — стандартная нормальная случайная величина. Пусть \((Y_n)_{n\ge 1}\) — i.i.d. последовательность с \(\mathbb E[Y_i^k]= \mathbb E[Z^k]\) для \(k=1,\ldots, \ell\). Пусть \(g\in C^\ell_b(\mathbb R)\). Докажите, что существует константа \(C\) (зависящая от \(g\) и распределения \(Y_i\)), такая что \[ \left| \mathbb E[g(S_n)]-\mathbb E[g(Z)] \right| \le C n^{-(\ell-1)/2} \]
Мартингальная версия
Стоит упомянуть, что Центральная предельная теорема выходит далеко за рамки независимых случайных величин. В конечном счёте, для такого типа результата даже не требуется, чтобы величины были определены на линейном пространстве (например, совершение малых случайных шагов на многообразии, по мере уменьшения шагов, будет сходиться к распределению на пространстве непрерывных кривых на многообразии, называемому броуновским движением). Таким образом, существуют сильные локальные версии ЦПТ, версии для метрических пространств, эргодические версии и так далее. Интересный пример, требующий лишь элементарных гипотез, охватывает случай мартингалов.
Теорема 3 (Центральная предельная теорема для мартингалов) Пусть \((X_n)_{n\ge 1}\) — последовательность вещественнозначных случайных величин и пусть \[ M_n:= X_1+\ldots+X_n \] Предположим, что
- \(\mathbb E[X_n| M_{n-1}]=0\).
- Для \(Q_n:= \mathbb E[X_n^2| M_{n-1} ]\), выполняется \(\sum_{n=1}^\infty Q_n=\infty\) п.н. (почти наверное).
- \(\mathbb E\left[\sup_n \mathbb E[|X_n|^3| M_{n-1} ] \right]<\infty\).
Пусть \(\tau_\ell:=\inf \{N\in \mathbb N \,:\: \sum_{n=1}^N Q_n \ge \ell\}\). Тогда \(M_{\tau_\ell}/\sqrt{\ell}\) сходится к стандартной нормальной величине по распределению при \(\ell \to \infty\).
Результаты о несходимости
Пока всё хорошо. Если \(Y_n\) — центрированные i.i.d. случайные величины с конечной дисперсией, то \(S_n\) сходится к нормальному пределу. По распределению. Будет ли эта сходимость иметь место по вероятности или даже п.н.?
Утверждение 1 Независимо от вероятностного пространства и распределения \(Y_n\), Центральная предельная теорема не выполняется по вероятности, даже для подпоследовательностей.
Суть в том, что если две последовательности \((S_n), (S_n')\) сходятся по вероятности, то \(S_n+S_n'\) также сходится по вероятности (по неравенству треугольника). То же утверждение неверно для сходимости по распределению, так как сходимость по распределению касается не самих случайных величин, а только их распределений. Таким образом, сходимость \(S_n\) или \(S_n'\) ничего не говорит об их совместном распределении.
Доказательство (Утверждение 1). Любая предельная точка (вдоль некоторой подпоследовательности) по вероятности \(S\) для \(S_n\) будет иметь стандартное нормальное распределение. В частности, \(\sqrt{2} S_{2n}-S_n\) сходилась бы к \((\sqrt{2}-1) S \sim \mathcal N(0,3-2\sqrt{2})\) по вероятности (вдоль той же подпоследовательности). Но \[ S_n':= \sqrt{2} S_{2n} - S_n = \frac{1}{\sqrt{n}}\sum_{i=n+1}^{2n} Y_i \] является суммой \(n\) i.i.d. величин, делённой на \(\sqrt{n}\), следовательно, Теорема 1 применима к \(S'_n\). А именно, для любой предельной точки \(S\), величина \((\sqrt{2}-1) S\) также должна иметь закон \(\mathcal{N}(0,1)\). Следовательно, предельных точек не существует.
Визуализация сходимости
Что означает, что последовательность сходится по распределению? Зафиксируем \(\mu\), центрированную вероятностную меру на \(\mathbb R\), и некоторое значение \(n\), ‘достаточно большое’ (как мы видели, насколько большое, зависит от \(\mu\), например, от её третьего момента), и рассмотрим i.i.d. величины \(X_1,\ldots,X_n\) с законом \(\mu\) и соответствующую им \(S_n\), как в Уравнение 1. Мы можем многократно, скажем \(N\) раз, независимо сгенерировать выборку \((X_1,\ldots,X_n)\) и, следовательно, \(S_n\). Центральная предельная теорема говорит нам, что с большой вероятностью доля выборок, для которых \(S_n\) попадает в заданный интервал \([a,b]\), приблизительно равна интегралу Гаусса по \([a,b]\). Здесь приблизительно означает, что вероятность этого события сходится к \(1\) по мере роста \(N\) и \(n\).
При большом \(n\) вероятность нахождения выборки в заданном интервале сходится к интегралу Гаусса по этому интервалу. В этом и заключается содержание центральной предельной теоремы. Здесь мы берём \(N\) выборок, строим гистограмму их распределения по интервалам и сравниваем результат с теоретической плотностью Гаусса.
#| '!! shinylive warning !!': |
#| shinylive does not work in self-contained HTML documents.
#| Please set `embed-resources: false` in your metadata.
#| standalone: true
#| components: [editor, viewer]
#| viewerHeight: 1080
#| editorHeight: 240
#| layout: vertical
# ========= 1. IMPORTS & CONFIGURATION =========
from shiny import App, render, ui, reactive, req
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, cauchy
# Configuration dictionary for UI inputs
DIST_CONFIG = {
'n_slider': {
'min': 10, 'max': 10000, 'value': 1000, 'step': 1,
},
'N_samples_slider': {
'min': 100, 'max': 10000, 'value': 5000, 'step': 100,
},
'distribution': {
'choices': ['{-1, +1} (Bernoulli)', 'Uniform [-1, 1]', 'Standard Normal N(0,1)', 'Centered Exponential (Exp(1)-1)', 'Standard Cauchy'],
'selected': '{-1, +1} (Bernoulli)',
},
'filename': {'value': 'clt_distribution.png'},
}
# ========= 2. UI DEFINITION =========
app_ui = ui.page_sidebar(
ui.sidebar(
ui.h4("Convergence in Distribution"),
ui.input_slider("n", "Sequence Length (n):", **DIST_CONFIG['n_slider']),
ui.input_slider("N_samples", "Number of Samples (N):", **DIST_CONFIG['N_samples_slider']),
ui.input_select("distribution", "Distribution:", **DIST_CONFIG['distribution']),
ui.hr(),
ui.input_action_button("run_button", "Run Simulation", class_="btn-success w-100"),
ui.hr(),
ui.h4("Saving Options"),
ui.input_checkbox("save_plot", "Save Plot", value=False),
ui.panel_conditional(
"input.save_plot",
ui.input_text("filename", "Filename:", **DIST_CONFIG['filename']),
),
title="Controls",
),
ui.output_plot("dist_plot", height="700px"),
title="Distribution of the Normalized Sum",
)
# ========= 3. SERVER LOGIC =========
def server(input, output, session):
# Reactive value to hold the generated matplotlib figure
figure_to_display = reactive.Value(None)
# --- Helper Functions (from original script) ---
def dist_generate_steps(dist_name, size):
if dist_name == '{-1, +1} (Bernoulli)': return np.random.choice([-1, 1], size=size)
if dist_name == 'Uniform [-1, 1]': return np.random.uniform(-1, 1, size=size)
if dist_name == 'Standard Normal N(0,1)': return np.random.randn(*size)
if dist_name == 'Centered Exponential (Exp(1)-1)': return np.random.standard_exponential(size=size) - 1
if dist_name == 'Standard Cauchy': return np.random.standard_cauchy(size=size)
raise ValueError(f"Unknown distribution: {dist_name}")
def dist_get_limit_pdf(dist_name, n):
if dist_name in ['{-1, +1} (Bernoulli)', 'Standard Normal N(0,1)', 'Centered Exponential (Exp(1)-1)']:
return 'Normal(0, 1)', lambda x: norm.pdf(x, loc=0, scale=1)
if dist_name == 'Uniform [-1, 1]':
# The variance of U[-1,1] is (1 - (-1))^2 / 12 = 4/12 = 1/3
return 'Normal(0, 1/√3)', lambda x: norm.pdf(x, loc=0, scale=np.sqrt(1/3))
if dist_name == 'Standard Cauchy':
# The normalized sum of Cauchy variables is still Cauchy.
# S_n / n ~ Cauchy(0,1), so S_n / sqrt(n) is not standard.
# Let's assume the user wants to see the stable distribution, which is just Cauchy.
return 'Cauchy(0, 1)', lambda x: cauchy.pdf(x, loc=0, scale=1)
@reactive.Effect
@reactive.event(input.run_button, ignore_init=True)
def _():
"""This function runs ONLY when the run_button is clicked."""
n = input.n()
N = input.N_samples()
dist_name = input.distribution()
try:
# Generate the sample data
X = dist_generate_steps(dist_name, size=(N, n))
# For Cauchy, the stable sum is normalized by n, not sqrt(n)
if dist_name == 'Standard Cauchy':
S_n_samples = np.sum(X, axis=1) / n
else:
S_n_samples = np.sum(X, axis=1) / np.sqrt(n)
# Create the plot
fig, ax = plt.subplots(figsize=(10, 6))
num_bins = min(150, max(20, N // 100))
ax.hist(S_n_samples, bins=num_bins, density=True, alpha=0.75, label=f'Empirical Dist. of $S_n$ (N={N:,})')
# Get and plot the theoretical PDF
limit_name, limit_pdf = dist_get_limit_pdf(dist_name, n)
x_min, x_max = ax.get_xlim()
# For Cauchy, the range can be very wide, so we limit it for plotting
if dist_name == 'Standard Cauchy':
x_min, x_max = -10, 10
x_axis = np.linspace(x_min, x_max, 400)
ax.plot(x_axis, limit_pdf(x_axis), 'r-', lw=2, alpha=0.9, label=f'Theoretical PDF: {limit_name}')
ax.set_title(f'Distribution of Normalized Sum for $X_i \\sim$ {dist_name}')
ax.set_xlabel('Value of the Normalized Sum')
ax.set_ylabel('Probability Density')
ax.legend()
ax.grid(True, linestyle='--', alpha=0.6)
ax.set_xlim(x_min, x_max) # Enforce x-limits
# Save if requested
if input.save_plot():
req(input.filename(), cancel_output=True)
fig.savefig(input.filename(), dpi=400, bbox_inches='tight')
# Update the reactive value to display the plot
figure_to_display.set(fig)
plt.close(fig)
except Exception as e:
fig, ax = plt.subplots()
ax.text(0.5, 0.5, f"An error occurred: {e}", ha='center', va='center', wrap=True)
figure_to_display.set(fig)
plt.close(fig)
@output
@render.plot
def dist_plot():
"""Renders the plot from the reactive value."""
fig = figure_to_display.get()
req(fig) # Do not render until the button is clicked
return fig
# ========= 4. APP INSTANTIATION =========
app = App(app_ui, server)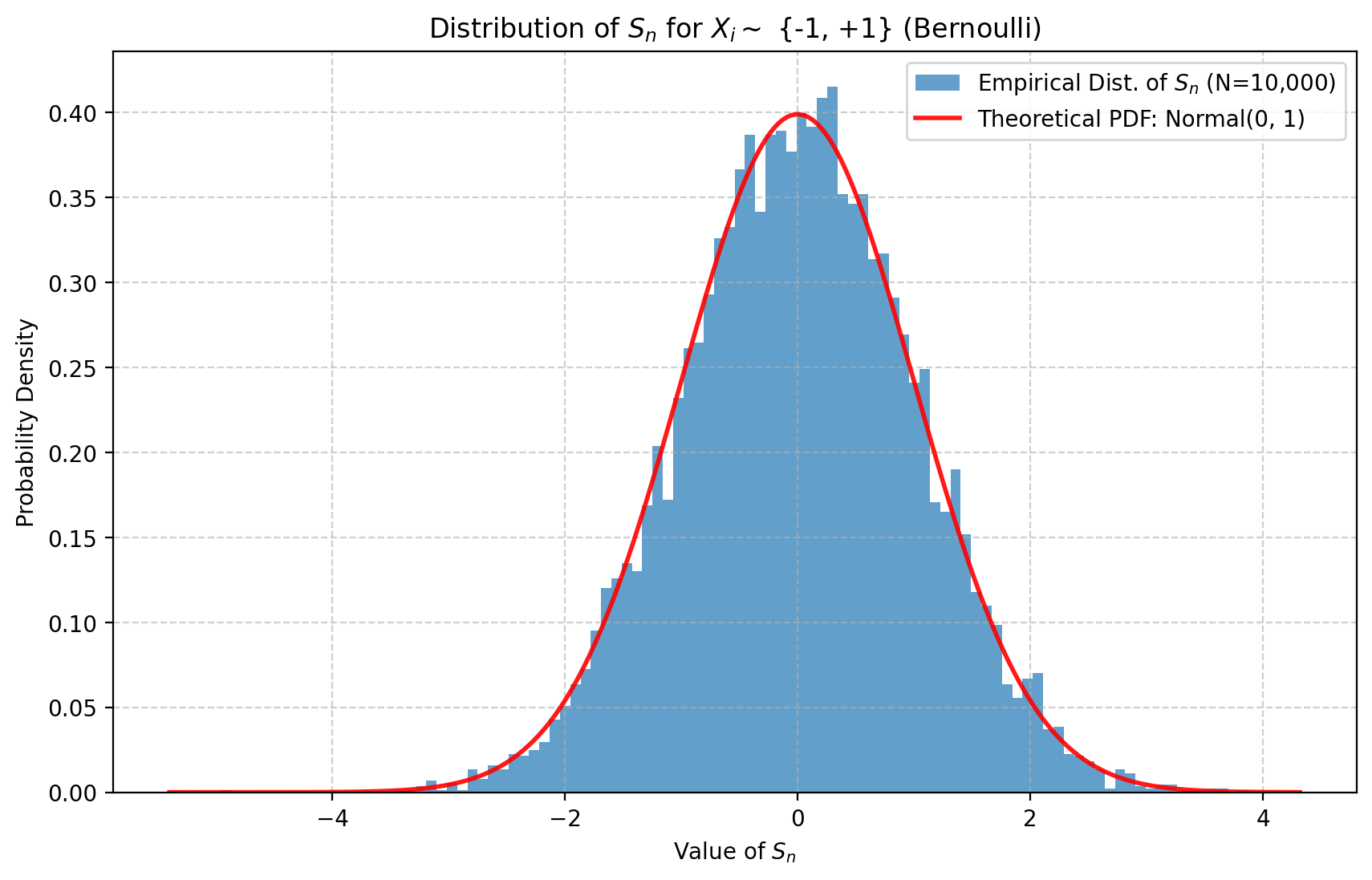
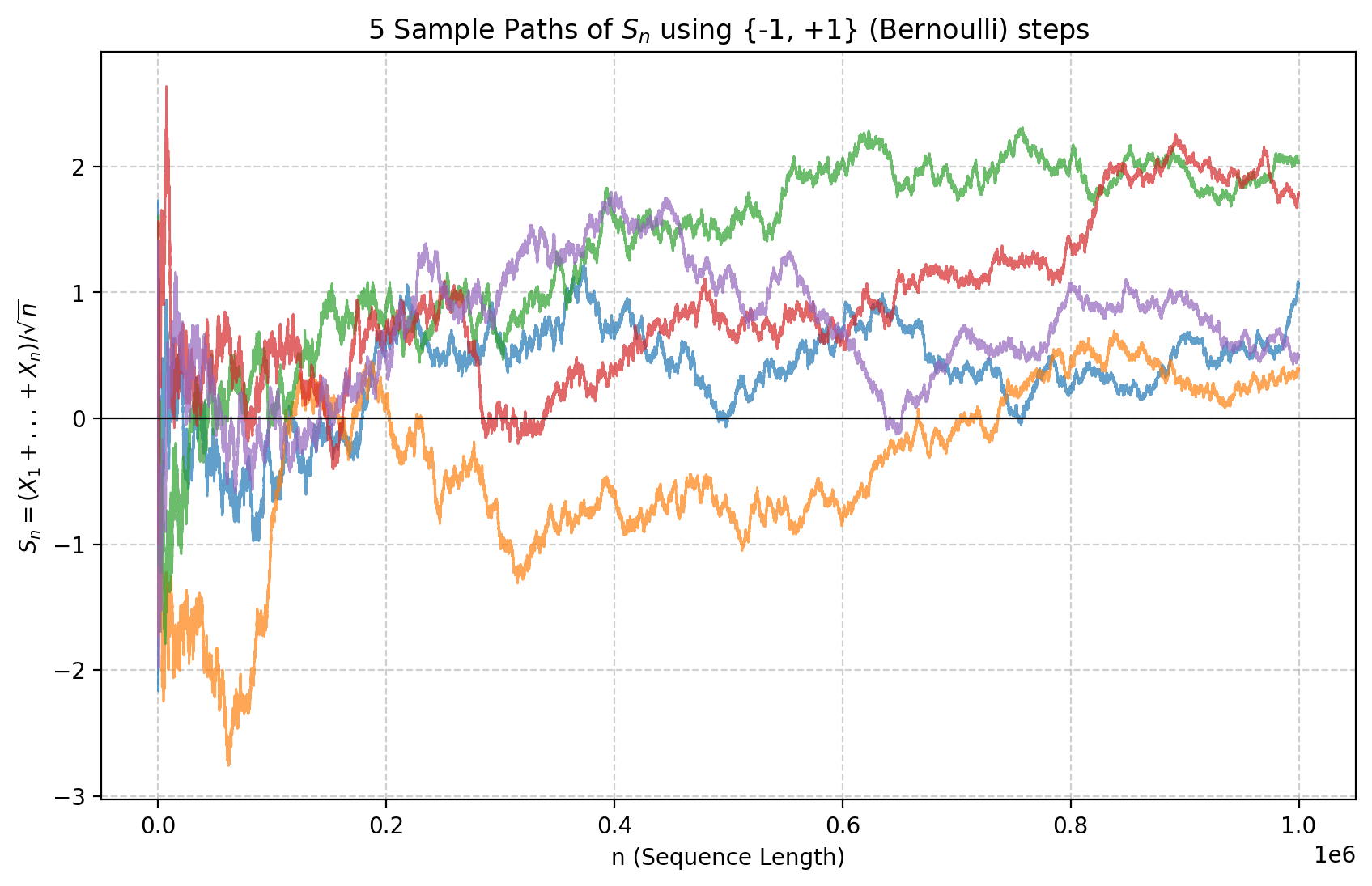
С другой стороны, тот факт, что \(S_n\) не сходится п.н., означает, что если мы зафиксируем одну реализацию (так сказать, одно \(\omega\)) и будем отслеживать значение \(S_n\) в зависимости от \(n\), оно не сойдётся ни к какому значению.
Каждая отдельная реализация не сходится как функция от \(n\). Мы генерируем \(X_i\) как i.i.d. и строим график \(S_n\) как функции от \(n\). Даже при больших \(n\) график колеблется, и сходимость не наступает.
#| '!! shinylive warning !!': |
#| shinylive does not work in self-contained HTML documents.
#| Please set `embed-resources: false` in your metadata.
#| standalone: true
#| components: [editor, viewer]
#| viewerHeight: 1080
#| editorHeight: 240
#| layout: vertical
# ========= 1. IMPORTS & CONFIGURATION =========
from shiny import App, render, ui, reactive, req
import numpy as np
import matplotlib.pyplot as plt
# Configuration dictionary for UI inputs
PATHS_CONFIG = {
'n_slider': {
'min': 1000, 'max': 1000000, 'value': 10000, 'step': 1000,
},
'N_slider': {
'min': 1, 'max': 50, 'value': 5, 'step': 1,
},
'distribution': {
'choices': ['{-1, +1} (Bernoulli)', 'Uniform [-1, 1]', 'Standard Normal N(0,1)', 'Standard Cauchy', 'Centered Exponential (Exp(1)-1)'],
'selected': 'Standard Normal N(0,1)',
},
'linewidth_slider': {
'min': 0.1, 'max': 3.0, 'value': 1.0, 'step': 0.1,
},
'filename': {'value': 'clt_paths.png'},
}
# ========= 2. UI DEFINITION =========
app_ui = ui.page_sidebar(
ui.sidebar(
ui.h4("Path Trajectory Simulation"),
ui.input_slider("n", "Sequence Length (n):", **PATHS_CONFIG['n_slider']),
ui.input_slider("N", "Number of Paths:", **PATHS_CONFIG['N_slider']),
ui.input_select("distribution", "Distribution:", **PATHS_CONFIG['distribution']),
ui.hr(),
ui.h4("Plotting & Saving Options"),
ui.input_slider("linewidth", "Line Width:", **PATHS_CONFIG['linewidth_slider']),
ui.input_action_button("resample_button", "Resample & Plot", class_="btn-success w-100"),
ui.hr(),
ui.input_checkbox("save_plot", "Save Plot", value=False),
ui.panel_conditional(
"input.save_plot",
ui.input_text("filename", "Filename:", **PATHS_CONFIG['filename']),
),
title="Controls",
),
ui.output_plot("paths_plot", height="600px"),
title="CLT Paths",
)
# ========= 3. SERVER LOGIC =========
def server(input, output, session):
# Reactive value to hold the generated matplotlib figure
figure_to_display = reactive.Value(None)
def paths_generate_steps(dist_name, size):
"""Generates random steps based on the selected distribution."""
if dist_name == '{-1, +1} (Bernoulli)':
return np.random.choice([-1, 1], size=size)
if dist_name == 'Uniform [-1, 1]':
return np.random.uniform(-1, 1, size=size)
if dist_name == 'Standard Normal N(0,1)':
return np.random.randn(*size)
if dist_name == 'Standard Cauchy':
return np.random.standard_cauchy(size=size)
if dist_name == 'Centered Exponential (Exp(1)-1)':
return np.random.standard_exponential(size=size) - 1
raise ValueError(f"Unknown distribution: {dist_name}")
@reactive.Effect
@reactive.event(input.resample_button, ignore_init=True)
def _():
"""This function runs ONLY when the resample_button is clicked."""
dist_name = input.distribution()
max_n = input.n()
N_trajectories = input.N()
line_width = input.linewidth()
try:
# Generate data
X = paths_generate_steps(dist_name, size=(N_trajectories, max_n))
cumulative_sums = np.cumsum(X, axis=1)
n_axis = np.arange(1, max_n + 1)
S_n = cumulative_sums / np.sqrt(n_axis)
# Create plot
fig, ax = plt.subplots(figsize=(10, 6))
for i in range(N_trajectories):
ax.plot(n_axis, S_n[i, :], alpha=0.7, linewidth=line_width)
ax.set_title(f'{N_trajectories} Sample Paths of $S_n$ using {dist_name} steps')
ax.set_xlabel('n (Sequence Length)')
ax.set_ylabel('$S_n = (X_1 + ... + X_n) / \\sqrt{n}$')
ax.grid(True, linestyle='--', alpha=0.6)
ax.axhline(0, color='black', linewidth=0.8)
# Save the plot if requested
if input.save_plot():
req(input.filename(), cancel_output=True)
fig.savefig(input.filename(), dpi=400, bbox_inches='tight')
# Set the reactive value, which will trigger the plot output to update
figure_to_display.set(fig)
# Close the figure object to free memory
plt.close(fig)
except Exception as e:
# On error, create a plot showing the error message
fig, ax = plt.subplots()
ax.text(0.5, 0.5, f"An error occurred: {e}", ha='center', va='center', wrap=True)
figure_to_display.set(fig)
plt.close(fig)
@output
@render.plot
def paths_plot():
"""Renders the plot held in the reactive value."""
fig = figure_to_display.get()
# Don't render anything until the button has been clicked at least once
req(fig)
return fig
# ========= 4. APP INSTANTIATION =========
app = App(app_ui, server)