Семинар 3

\[\newcommand{\st}{\, : \:} \newcommand{\ind}[1]{\mathbf{1}_{#1}} \newcommand{\dd}{\mathrm{d}}\]

Задача 1

При прохождении одного порога байдарка не получает повреждений с вероятностью \(p_1\), получает серьезные повреждения с вероятность \(p_2\), и полностью ломается с вероятностью \(p_3 = 1-p_1-p_2\). Два серьезных повреждения приводят к полной поломке. Найдите вероятность того, что при прохождении \(n\) порогов байдарка не будет полностью сломана.

СоветРешение

Пусть состояние байдарки после \(k\) порогов описывается числом полученных серьезных повреждений. Состояние “сломана” — это отдельное состояние. Обозначим:

• \(a_k\): вероятность, что после \(k\) порогов у байдарки нет повреждений.
• \(b_k\): вероятность, что после \(k\) порогов у байдарки одно серьезное повреждение.
• \(c_k\): вероятность, что после \(k\) порогов байдарка сломана.

ясно \(a_n=p_1^n\) и \(b_n=n p_1^{n-1} p_2\). Вероятность того, что байдарка не сломана после \(n\) порогов, равна \(a_n + b_n= p_1^{n-1}(p_1+n p_2)\).

но применим более общий подход. Начальные условия: \(a_0 = 1, b_0 = 0, c_0 = 0\). Рекуррентные соотношения:

• Байдарка остается без повреждений, только если она была без повреждений и не получила их на следующем пороге: \(a_k = a_{k-1} \cdot p_1\). Отсюда \(a_n = p_1^n\).
• Байдарка получает первое серьезное повреждение, если она была без повреждений и получила его, либо она уже имела одно повреждение и не получила нового: \(b_k = a_{k-1} \cdot p_2 + b_{k-1} \cdot p_1\).
• Байдарка ломается, если она уже была сломана, или была без повреждений и сломалась, или имела одно повреждение и получила еще одно или сломалась: \(c_k = c_{k-1} + a_{k-1} \cdot p_3 + b_{k-1} \cdot (p_2 + p_3)\).

Затем мы можем найти \(a_n\) и \(b_n\), как указано выше, методом индукции.

Задача 2

Пусть \(n \ge 2\). Случайным образом выбираем из \({1, 2,\ldots,n}\) одно число. Событие \(A\) — выбранное число делится на \(2\), событие \(B\) — выбранное число делится на \(7\). Найдите все \(n\) такие, что события \(A\) и \(B\) независимы.

СоветРешение

Нам нужно решить \[ \lfloor n/14 \rfloor / n = \mathbb{P}(A\cap B) =^? \mathbb{P}(A) \mathbb{P}(B) = \lfloor n/2 \rfloor \lfloor n/7 \rfloor / n^2 \] Запишите \(n=14*k+r\), с \(0 \le r \le 13\), чтобы получить \[ k r = 2k \lfloor r/2 \rfloor +7k \lfloor r/7 \rfloor + \lfloor r/7 \rfloor \lfloor r/2 \rfloor \] что выполняется, если \(k=0\) и \(n=r\le 6\), или если \(k\ge 1\) и \(r=0,2,4,6\). Поэтому ответ: \(n=0,2,4,6\pmod 14\) или \(n=3,5\).

Задача 3

(геометрическое распределение) Два игрока по очереди подбрасывают кость. Тот, у кого первого выпало 6, — проиграл.

1. Найдите вероятность произвести за кон ровно \(n\) бросаний.
2. Найдите вероятность того, что первый игрок проиграл.

СоветРешение

1. Чтобы было ровно \(n\) бросков, \((n-1)\)-й раз результат не должен быть 6, а \(n\)-й раз должен быть 6. Таким образом, вероятность равна \((5/6)^{n-1} 1/6\).
2. Из предыдущего пункта следует, что игра закончится с вероятностью \(1\). Пусть \(p\) — вероятность победы первого игрока. Тогда, исходя из первого результата, \((1-p)=1/6+(5/6) p\), и \(p=5/11\).

Задача 4

1. Пусть событие \(A\) не зависит само от себя. Чему равна его вероятность?
2. Пусть \(\mathbb{P}(A) = 0\) или \(\mathbb{P}(A) = 1\). Покажите, что событие \(A\) независимо с любым событием \(B\).

СоветРешение

1. По определению независимости, \(\mathbb{P}(A \cap A) = \mathbb{P}(A) \cdot \mathbb{P}(A)\). Поскольку \(A \cap A = A\), это означает \(\mathbb{P}(A) = (\mathbb{P}(A))^2\). Таким образом, вероятность такого события может быть только \(0\) или \(1\).
2. Если \(\mathbb{P}(A) = 0\), то \(0 \le \mathbb{P}(A \cap B) \le \mathbb{P}(A) = 0 =\mathbb{P}(A) \mathbb{P}(B)\). Если \(\mathbb{P}(A)=1\), то \(\mathbb{P}(A^c)=0\), поэтому \(A^c\) и \(B\) независимы. Следовательно, \(A\) и \(B\) независимы.

Задача 5

Кубик бросают до тех пор, пока впервые не выпадет меньше \(5\) очков. Какова вероятность получить при последнем броске не меньше \(2\) очков?

СоветРешение

Прежде всего, заметим, что игра останавливается с вероятностью \(1\), поэтому «последний бросок» четко определен. В последнем броске мы с равной вероятностью получаем одно из значений \(\{1,2,3,4\}\), и нас просят найти вероятность того, что это значение будет не меньше \(2\), а именно из множества \(\{2,3,4\}\). Таким образом, ответ \(3/4\).

Мы можем формализовать это интуитивное решение. Пусть \(A_k\) — событие, при котором игра останавливается на \(k\)-м броске, а \(B\) — событие, что при последнем броске выпало не меньше \(2\). Тогда \(\mathbb{P}(B|A_k)=3/4\), так как это в точности вероятность того, что на \(k\)-м броске мы получили не меньше \(2\), зная, что мы получили не больше \(4\). Тогда \[ \mathbb{P}(B)=\sum_k \mathbb{P}(B|A_k) \mathbb{P}(A_k)= 3/4 \sum_k \mathbb{P}(A_k) =3/4 \] Таким образом, первоначальная интуиция верна, нам не нужно вычислять точное значение \(\mathbb{P}(A_k)\), нам просто нужно знать, что сумма этих вероятностей равна \(1\), а именно, что игра закончится с вероятностью \(1\).

Задача 6

Алиса и Боб играют в следующую игру. Бросается правильная монета до тех пор пока не встретится комбинация 110 или 100. Алиса выигрывает, если первой появилась комбинация 110, а Боб в случае, когда первой появилась комбинация 100. Кто будет выигрывать чаще? Какая вероятность побед Алисы и Боба?

СоветРешение

Пусть \(p_{x_1 x_2 \ldots}\) — вероятность того, что Алиса выиграет, если (при условии, что) первые броски были \(x_1, x_2,\ldots\), и пусть \(p=p_{\emptyset}\) — вероятность выигрыша Алисы. Например, \(p_{10}\) — это вероятность того, что Алиса выиграет, если первые два результата были \(1,0\). Тогда мы имеем \(p_{0}=p\), \(p_{11}=1\), \(p_{100}=0\), \(p_{101}=p_1\). Теперь мы можем обусловить по предыдущим результатам, чтобы получить \[ \begin{aligned} & p= \tfrac{1}{2} p_0 + \tfrac{1}{2} p_1 = (p+p_1)/2 \\ & p_1 = \tfrac{1}{2} p_11 + \tfrac{1}{4}p_{100}+\tfrac{1}{4}p_{101}= (2+0+p_1)4 \end{aligned} \] Это дает \(p_1=p=2/3\).

Задача 7

Пусть \(p_n\) обозначает вероятность того, что за \(n\) подбрасываний симметричной монеты ни разу не выпадут три орла подряд. Найдите рекурсию для \(p_n\).

СоветРешение

Пусть \(B_n\) — событие, при котором в \(n\) бросках нет трех орлов подряд, а \(A_k\) — событие, при котором первая решка выпадает на \(k\)-й позиции. Мы имеем, что \(\mathbb{P}(B_n|A_k)=0\) для \(k>3\), в то время как \(\mathbb{P}(B_n|A_k)=\mathbb{P}(B_{n-k})\) для \(k=1,2,3\). Следовательно \[ p_n = \mathbb{P}(B_n)= \sum_{k} \mathbb{P}(B_n|A_k) \mathbb{P}(A_k) = \frac{1}{2} p_{n-1} + \frac{1}{4} p_{n-2} + \frac{1}{8} p_{n-3}, \quad \text{for } n \ge 3. \] Начальные условия: \(p_0=p_1=p_2=1\).

Задача 8

События \(A\), \(B\), \(C\) попарно независимы и равновероятны, \(A\cap B \cap C =\emptyset\). Найдите максимально возможное значение \(P(A)\).

СоветРешение

Пусть \(p=P(A)=P(B)=P(C)\). Тогда \[ (1-p)^2=P(\bar{B}\cap \bar{C}) \ge P(\bar{A}\cap \bar{B}\cap \bar{C})=1-P(A\cup B\cup C)=1-(3p-3p^2+0) \] Отсюда следует, что \(p\le 1/2\). Легко проверить, что \(p=1/2\) возможно. Например, \(\Omega=\{1,2,3,4\}\) с равномерной вероятностью, и \(A=\{1,2\}, B=\{1,3\}, C=\{2,3\}\).

Задача 9

Согласно расписанию, автобус и троллейбус ходят каждые 20 минут до полуночи, троллейбус начинает движение в 6:00, а автобус – в 6.15. Найти вероятность уехать троллейбусом, придя на остановку в случайный момент времени днем и выбрав первый подошедший транспорт.

СоветРешение

В силу периодичности (рассматривая по модулю \(20\) минут), мы можем ограничиться одним 20-минутным интервалом, скажем, \([0,20]\). Будем считать, что прибытие в случайный момент времени означает, что вероятность прибытия в заданный интервал пропорциональна его длине. Поскольку мы уезжаем на троллейбусе тогда и только тогда, когда прибываем в интервале \((15,20]\), вероятность этого равна \(5/20 = 1/4\).

Задача 10

\(X\) и \(Y\) договорились встретиться в промежуток времени с 12.00 до 13.00, причем каждый из них готов ждать ровно \(30\) минут. Какова вероятность встречи? Какова вероятность того, что они встретились и \(X\) не ждал \(Y\)? Какова вероятность, что они пришли одновременно?

СоветРешение

Будем измерять всё в часах от 12:00. Пусть \(X\) и \(Y\) — время прибытия двух людей. Они независимы и равномерно распределены на интервале \([0,1]\) часа. Пространство элементарных исходов — это квадрат \(\Omega=[0,1] \times [0,1]\) с площадью \(1\). Следовательно, вероятность события в \(\Omega\) — это его мера Лебега.

• Они встретятся тогда и только тогда, когда \(|X - Y| \le 0.5\). Таким образом, \(\mathbb{P}(|X - Y| \le 0.5)=3/4\).
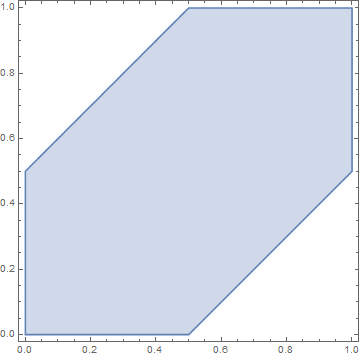
• Они встретятся и \(X\) не будет ждать \(Y\) тогда и только тогда, когда \(0\le X-Y \le 0.5\).
• Вероятность того, что они прибудут одновременно, \(X=Y\), — это площадь диагонали квадрата, то есть \(0\).

Задача 11

Стандартный компьютерный генератор rand выдает случайные числа на интервале \([0,1]\), далее из каждого извлекают квадратный корень и ответ печатают в формате с фиксированной точкой, используя точность 16 знаков после запятой (то есть например, так: \(0.0003267891135015\ldots\)). Найти вероятность, что в этой записи второй цифрой после десятичной точки будет двойка? Найдите ответ аналитически и сравните с результатом компьютерного эксперимента.

СоветРешение

Пусть \(X\) — результат генерации, а \(Y = \sqrt{X}\). \(\mathbb{P}(Y\in [a,b)) =\mathbb{P}(X\in [a^2,b^2))=b^2-a^2\). Таким образом, \[ \mathbb{P}\left(Y\in \cup_{k=0}^9 [\frac{10k+3}{100},\frac{10k+2}{100})\right)= 10^{-4}\sum_{k=0}^9 20k+5 = 95/1000=0.095 \]

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| standalone: true
#| components: [editor, viewer]
#| viewerHeight: 1080
#| editorHeight: 240
#| layout: vertical

from shiny import App, render, ui, reactive, req
import numpy as np
import matplotlib.pyplot as plt
import math

# ========= 1. UI DEFINITION =========
app_ui = ui.page_sidebar(
    ui.sidebar(
        ui.h4("Probability Experiment Controls"),
        ui.input_slider("q", "Power (q):", min=0.1, max=10.0, value=0.5, step=0.1),
        ui.input_slider("k", "Digit Position (k):", min=1, max=10, value=2, step=1),
        ui.input_slider("r", "Base (r):", min=2, max=16, value=10, step=1),
        ui.input_slider("d", "Digit (d):", min=0, max=15, value=2, step=1),
        ui.input_slider("N", "Number of Tries (N):", min=100, max=10000, value=1000, step=100),
        ui.input_action_button("run_simulation", "Run Simulation", class_="btn-success"),
        title="Controls",
    ),
    ui.output_text("probability_result"),
    ui.output_plot("digit_distribution_plot", height="600px"),
    title="Experimental Probability Calculator",
)

# ========= 2. SERVER LOGIC =========
def server(input, output, session):
    simulation_results = reactive.Value(None)

    def get_kth_digit(num, k, r):
        """Calculates the k-th digit of num in base r after the decimal point."""
        # Multiply by r^k to shift the desired digit to the integer part
        shifted_num = num * (r**k)
        # Take the floor to isolate the integer part
        integer_part = math.floor(shifted_num)
        # The k-th digit is the last digit of this integer part
        return integer_part % r

    @reactive.Effect
    @reactive.event(input.run_simulation, ignore_init=True)
    def _():
        """This function runs ONLY when the run_simulation button is clicked."""
        q = input.q()
        k = input.k()
        r = input.r()
        d = input.d()
        N = input.N()
        
        # Ensure the chosen digit 'd' is valid for the base 'r'
        if d >= r:
            simulation_results.set({"error": f"Digit (d={d}) must be less than the base (r={r})."})
            return

        # Generate N random numbers in [0, 1]
        random_numbers = np.random.rand(N)
        
        # Compute Y = X^q
        powered_numbers = np.power(random_numbers, q)
        
        # Find the k-th digit for each number
        digits = [get_kth_digit(y, k, r) for y in powered_numbers]
        
        # Count matches
        matches = sum(1 for digit in digits if digit == d)
        
        # Calculate probability
        probability = matches / N if N > 0 else 0
        
        # Store results for rendering
        simulation_results.set({
            "probability": probability,
            "digits": digits,
            "base": r,
            "d": d,
            "k": k,
            "q": q
        })

    @output
    @render.text
    def probability_result():
        results = simulation_results.get()
        if not results:
            return "Click 'Run Simulation' to see the results."
        if "error" in results:
            return f"Error: {results['error']}"
        
        prob = results["probability"]
        d = results["d"]
        k = results["k"]
        return f"Experimental Probability of the {k}-th digit being {d}: {prob:.4f}"

    @output
    @render.plot
    def digit_distribution_plot():
        results = simulation_results.get()
        req(results)
        if "error" in results:
            # Create a blank plot in case of an error
            fig, ax = plt.subplots()
            ax.text(0.5, 0.5, f"Error: {results['error']}", ha='center', va='center', color='red')
            return fig

        digits = results["digits"]
        r = results["base"]
        
        # Create a histogram of the digit frequencies
        fig, ax = plt.subplots(figsize=(8.5, 6))
        counts, bins, patches = ax.hist(digits, bins=np.arange(r + 1) - 0.5, rwidth=0.8, align='mid', color='royalblue', alpha=0.7)
        ax.set_xticks(range(r))
        ax.set_xlabel("Digit", fontsize=12)
        ax.set_ylabel("Frequency", fontsize=12)
        ax.set_title(f"Distribution of the {results['k']}-th Digit in Base {r}", fontsize=14)
        ax.grid(True, linestyle='--', alpha=0.5)

        # Highlight the bar for the chosen digit 'd'
        d = results["d"]
        if d < len(patches):
            patches[d].set_fc('salmon')
            
        return fig

# ========= 3. APP INSTANTIATION =========
app = App(app_ui, server)

Задача 12

Трое загадывают по числу из отрезка \([0, 1]\). Какова вероятность того, что существует треугольник с такими сторонами?

СоветРешение

Три числа являются длинами сторон треугольника тогда и только тогда, когда наибольшее из них не превышает суммы двух других. Другими словами, нам нужно вычислить объём области \(\{\max\{x,y,z\}\le (x+y+z)/2\}\) внутри единичного куба \([0,1]^3\). Дополнение состоит из трех непересекающихся областей \(x+y \le z\), \(x+z \le y\) и \(y+z \le x\). Каждая из этих областей является тетраэдром с объемом \(1/6\). Таким образом, общий объём «неудачной» области составляет \(3 \cdot (1/6) = 1/2\). Вероятность того, что числа образуют треугольник, равна \(1-1/2 = 1/2\).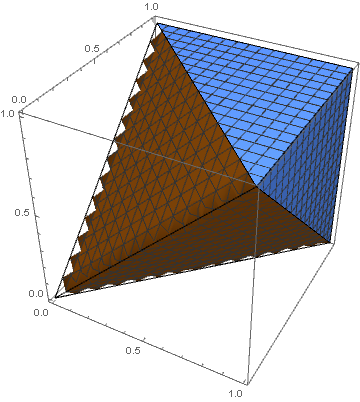

В качестве альтернативы, каждая из \(6\) перестановок, упорядочивающих три числа, имеет одинаковую вероятность. Таким образом, мы можем вычислить меру множества \(\{(x,y,z)\in [0,1]^3 \, :\: x\le y \le z \le x+y\}\), а именно \[ p= 6 \int_0^1 dx \int_x^1 dy \int_y^{\min(x+y,1)} dz=6 \int_0^1 dx \int_x^1 (\min(x+y,1)-y) dy = 1/2 \]