Seminar 3

\[\newcommand{\st}{\, : \:} \newcommand{\ind}[1]{\mathbf{1}_{#1}} \newcommand{\dd}{\mathrm{d}}\]

Exercice 1

When passing one rapid, a kayak sustains no damage with probability $p_1$, receives serious damage with probability $p_2$, and breaks completely with probability $p_3 = 1-p_1-p_2$. Two serious damages lead to a complete breakage. Find the probability that after passing $n$ rapids, the kayak will not be completely broken.

Solution

Let the state of the kayak after $k$ rapids be described by the number of serious damages it has sustained. The ‘broken’ state is a separate state. Let’s denote:

$a_k$: the probability that after $k$ rapids the kayak has no damage.
$b_k$: the probability that after $k$ rapids the kayak has one serious damage.
$c_k$: the probability that after $k$ rapids the kayak is broken.

Clearly, $a_n=p_1^n$ and $b_n=n p_1^{n-1} p_2$. The probability that the kayak is not broken after $n$ rapids is $a_n + b_n= p_1^{n-1}(p_1+n p_2)$.

But let’s apply a more general approach. Initial conditions: $a_0 = 1, b_0 = 0, c_0 = 0$. Recurrence relations:

The kayak remains undamaged only if it was undamaged and did not receive any damage on the next rapid: $a_k = a_{k-1} \cdot p_1$. From this, $a_n = p_1^n$.
The kayak has one serious damage if it was undamaged and received a serious one, or if it already had one serious damage and passed the next rapid without any damage: $b_k = a_{k-1} \cdot p_2 + b_{k-1} \cdot p_1$.
The kayak breaks if it was already broken, or if it was undamaged and broke, or if it had one damage and received another one or broke: $c_k = c_{k-1} + a_{k-1} \cdot p_3 + b_{k-1} \cdot (p_2 + p_3)$.

We can then find $a_n$ and $b_n$ as above by induction.

Exercice 2

Let $n \ge 2$. A number is chosen randomly from ${1, 2,\ldots,n}$. Event $A$ is that the chosen number is divisible by $2$, and event $B$ is that the chosen number is divisible by $7$. Find all $n$ such that events $A$ and $B$ are independent.

Solution

We need to solve \[ \lfloor n/14 \rfloor / n = \mathbb{P}(A\cap B) =^? \mathbb{P}(A) \mathbb{P}(B) = \lfloor n/2 \rfloor \lfloor n/7 \rfloor / n^2 \] Write $n=14k+r$, with $0 \le r \le 13$, to get \[ k r = 2k \lfloor r/2 \rfloor +7k \lfloor r/7 \rfloor + \lfloor r/7 \rfloor \lfloor r/2 \rfloor \] which holds if $k=0$ and $n=r\le 6$, or if $k\ge 1$ and $r=0,2,4,6$. Therefore, the answer is: $n \equiv 0,2,4,6 \pmod{14}$ or $n=3,5$.

Exercice 3

(Geometric distribution) Two players take turns rolling a die. The first one to roll a 6 loses.

Find the probability that a round consists of exactly $n$ rolls.
Find the probability that the first player loses.

Solution

For there to be exactly $n$ rolls, the first $(n-1)$ rolls must not be 6, and the $n$-th roll must be a 6. Thus, the probability is $(5/6)^{n-1} 1/6$.
From the previous part, it follows that the game ends with probability 1. Let $p$ be the probability that the first player wins. Then, based on the first roll, $1-p=1/6+(5/6) p$, and $p=6/11$.

Exercice 4

Let event $A$ be independent of itself. What is its probability?
Let $\mathbb{P}(A) = 0$ or $\mathbb{P}(A) = 1$. Show that event $A$ is independent of any event $B$.

Solution

By the definition of independence, $\mathbb{P}(A \cap A) = \mathbb{P}(A) \cdot \mathbb{P}(A)$. Since $A \cap A = A$, this means $\mathbb{P}(A) = (\mathbb{P}(A))^2$. Therefore, the probability of such an event can only be $0$ or $1$.
If $\mathbb{P}(A) = 0$, then $0 \le \mathbb{P}(A \cap B) \le \mathbb{P}(A) = 0 =\mathbb{P}(A) \mathbb{P}(B)$. If $\mathbb{P}(A)=1$, then $\mathbb{P}(A^c)=0$, so $A^c$ and $B$ are independent. Therefore, $A$ and $B$ are independent.

Exercice 5

A die is rolled until a number less than $5$ is obtained for the first time. What is the probability that the last roll is at least $2$?

Solution

First notice that the game stops with probability $1$, so “the last roll” is well defined. The last time we roll the die, we have got ${1,2,3,4}$ with equal probability, and we are asking the probability that this is at least $2$, namely ${2,3,4}$. The answer is then $3/4$.

We can formalize this intuitive solution. Let’s call $A_k$ the event on which the game stops at the $k$-th toss, and $B$ the event that, at the last toss, we got $2$. Then $\mathbb{P}(B|A_k)=3/4$, since this is exactly the probability that at the $k$-th toss we got at least $2$, knowing that we got no more than $4$. Then \[ \mathbb{P}(B)=\sum_k \mathbb{P}(B|A_k) \mathbb{P}(A_k)= 3/4 \sum_k \mathbb{P}(A_k) =3/4 \] So the initial intuition is correct, we do not need to compute the exactly value of $\mathbb{P}(A_k)$, we just need to know that the sum of those probabilities is $1$, namely that the game will end with probability $1$.

Exercice 6

Alice and Bob play the following game. A fair coin is tossed until the sequence 110 or 100 appears. Alice wins if 110 appears first, and Bob wins if 100 appears first. Who will win more often? What are the probabilities of Alice’s and Bob’s wins?

Solution

Let $p_{x_1 x_2 \ldots}$ be the probability that Alice wins if (conditionally on) the first tosses were $x_1, x_2,\ldots$, and let $p=p_{\emptyset}$ be the probability that Alice wins. For instance $p_{10}$ is the probability that Alice wins if the first two results are $1,0$. Then we have $p_{0}=p$, $p_{11}=1$, $p_{100}=0$, $p_{101}=p_1$. We can know condition on the previous results to get \[ \begin{aligned} & p= \tfrac{1}{2} p_0 + \tfrac{1}{2} p_1 = (p+p_1)/2 \\ & p_1 = \tfrac{1}{2} p_11 + \tfrac{1}{4}p_{100}+\tfrac{1}{4}p_{101}= (2+0+p_1)4 \end{aligned} \] This gives $p_1=p=2/3$.

Exercice 7

Let $p_n$ denote the probability that in $n$ tosses of a fair coin, three consecutive heads do not appear. Find a recurrence relation for $p_n$.

Solution

Let $B_n$ be the event where there are not three consecutive heads in $n$ tosses and $A_k$ the event where the first tail is at position $k$. We have that $\mathbb{P}(B_n|A_k)=0$ for $k>3$, while $\mathbb{P}(B_n|A_k)=\mathbb{P}(B_{n-k})$ for $k=1,2,3$. Therefore \[ p_n = \mathbb{P}(B_n)= \sum_{k} \mathbb{P}(B_n|A_k) \mathbb{P}(A_k) = \frac{1}{2} p_{n-1} + \frac{1}{4} p_{n-2} + \frac{1}{8} p_{n-3}, \quad \text{for } n \ge 3. \] The initial conditions are $p_0=p_1=p_2=1$.

Exercice 8

Events $A$, $B$, $C$ are pairwise independent and equally likely, $A\cap B \cap C =\emptyset$. Find the maximum possible value of $P(A)$.

Solution

Let $p=P(A)=P(B)=P(C)$. Then \[ (1-p)^2=P(\bar{B}\cap \bar{C}) \ge P(\bar{A}\cap \bar{B}\cap \bar{C})=1-P(A\cup B\cup C)=1-(3p-3p^2+0) \] As a consequence, $p\le 1/2$. It is easy to check that $p=1/2$ is possible. E.g. $\Omega=\{1,2,3,4\}$ with uniform probability, and $A=\{1,2\}, B=\{1,3\}, C=\{2,3\}$.

Exercice 9

According to the schedule, a tram and a trolleybus run every 20 minutes until midnight. The trolleybus starts at 6:00, and the tram at 6:15. Find the probability of leaving by trolleybus, if you arrive at the stop at a random time during the day and take the first vehicle that arrives.

Solution

Due to periodicity (reason $\pmod 20$ minutes), we can restrict to one interval of $20$ minutes, say $[0,20]$. We understand that arriving at a random time means that the probability of arriving in a given interval, is proportional to the length of that interval. Since we leave by trolleybus iff we arrive in the interval $(15,20]$, the probability is $1/4$.

Exercice 10

$X$ and $Y$ agreed to meet between 12:00 and 13:00. Each is willing to wait for exactly $30$ minutes. What is the probability that they meet? What is the probability that they meet and $X$ did not wait for $Y$? What is the probability that they arrive at the same time?

Solution

Let’s measure everything in hours from time 12:00. Let’s call $X$ and $Y$ the arrival times of the two persons. They are independent and uniformly distributed on the interval $[0,1]$ hours. The sample space is the square $\Omega=[0,1] \times [0,1]$ with area $1$. The probability of an event in $\Omega$ is therefore its Lebesgue measure.

They will meet iff $|X - Y| \le 0.5$. Thus $\mathbb{P}(|X - Y| \le 0.5)= 3/4$.
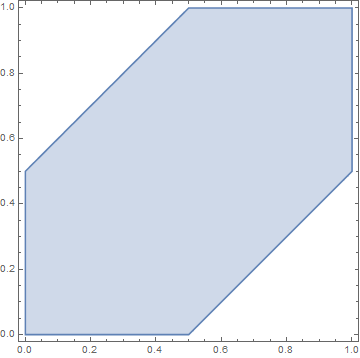
They will meet and $X$ did not wait for $Y$ iff $0\le X-Y \le 0.5$.
The probability that they arrive at the same time, $X=Y$, is the area of the diagonal of the square, namely $0$.

Exercice 11

A standard computer generator rand produces random numbers on the interval $[0,1]$. Then, the square root of each number is taken, and the answer is printed in a fixed-point format with 16 digits of precision after the decimal point (e.g., like this: $0.0003267891135015\ldots$). Find the probability that in this notation, the second digit after the decimal point will be a two. Find the answer analytically and compare it with the result of a computer experiment.

Solution

Let $X$ be the result of the generation, and $Y = \sqrt{X}$. $\mathbb{P}(Y\in [a,b)) =\mathbb{P}(X\in [a^2,b^2))=b^2-a^2$. Thus \[ \mathbb{P}\left(Y\in \cup_{k=0}^9 [\frac{10k+3}{100},\frac{10k+2}{100})\right)= 10^{-4}\sum_{k=0}^9 20k+5 = 95/1000=0.095 \]

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| standalone: true
#| components: [editor, viewer]
#| viewerHeight: 1080
#| editorHeight: 240
#| layout: vertical

from shiny import App, render, ui, reactive, req
import numpy as np
import matplotlib.pyplot as plt
import math

# ========= 1. UI DEFINITION =========
app_ui = ui.page_sidebar(
    ui.sidebar(
        ui.h4("Probability Experiment Controls"),
        ui.input_slider("q", "Power (q):", min=0.1, max=10.0, value=0.5, step=0.1),
        ui.input_slider("k", "Digit Position (k):", min=1, max=10, value=2, step=1),
        ui.input_slider("r", "Base (r):", min=2, max=16, value=10, step=1),
        ui.input_slider("d", "Digit (d):", min=0, max=15, value=2, step=1),
        ui.input_slider("N", "Number of Tries (N):", min=100, max=10000, value=1000, step=100),
        ui.input_action_button("run_simulation", "Run Simulation", class_="btn-success"),
        title="Controls",
    ),
    ui.output_text("probability_result"),
    ui.output_plot("digit_distribution_plot", height="600px"),
    title="Experimental Probability Calculator",
)

# ========= 2. SERVER LOGIC =========
def server(input, output, session):
    simulation_results = reactive.Value(None)

    def get_kth_digit(num, k, r):
        """Calculates the k-th digit of num in base r after the decimal point."""
        # Multiply by r^k to shift the desired digit to the integer part
        shifted_num = num * (r**k)
        # Take the floor to isolate the integer part
        integer_part = math.floor(shifted_num)
        # The k-th digit is the last digit of this integer part
        return integer_part % r

    @reactive.Effect
    @reactive.event(input.run_simulation, ignore_init=True)
    def _():
        """This function runs ONLY when the run_simulation button is clicked."""
        q = input.q()
        k = input.k()
        r = input.r()
        d = input.d()
        N = input.N()
        
        # Ensure the chosen digit 'd' is valid for the base 'r'
        if d >= r:
            simulation_results.set({"error": f"Digit (d={d}) must be less than the base (r={r})."})
            return

        # Generate N random numbers in [0, 1]
        random_numbers = np.random.rand(N)
        
        # Compute Y = X^q
        powered_numbers = np.power(random_numbers, q)
        
        # Find the k-th digit for each number
        digits = [get_kth_digit(y, k, r) for y in powered_numbers]
        
        # Count matches
        matches = sum(1 for digit in digits if digit == d)
        
        # Calculate probability
        probability = matches / N if N > 0 else 0
        
        # Store results for rendering
        simulation_results.set({
            "probability": probability,
            "digits": digits,
            "base": r,
            "d": d,
            "k": k,
            "q": q
        })

    @output
    @render.text
    def probability_result():
        results = simulation_results.get()
        if not results:
            return "Click 'Run Simulation' to see the results."
        if "error" in results:
            return f"Error: {results['error']}"
        
        prob = results["probability"]
        d = results["d"]
        k = results["k"]
        return f"Experimental Probability of the {k}-th digit being {d}: {prob:.4f}"

    @output
    @render.plot
    def digit_distribution_plot():
        results = simulation_results.get()
        req(results)
        if "error" in results:
            # Create a blank plot in case of an error
            fig, ax = plt.subplots()
            ax.text(0.5, 0.5, f"Error: {results['error']}", ha='center', va='center', color='red')
            return fig

        digits = results["digits"]
        r = results["base"]
        
        # Create a histogram of the digit frequencies
        fig, ax = plt.subplots(figsize=(8.5, 6))
        counts, bins, patches = ax.hist(digits, bins=np.arange(r + 1) - 0.5, rwidth=0.8, align='mid', color='royalblue', alpha=0.7)
        ax.set_xticks(range(r))
        ax.set_xlabel("Digit", fontsize=12)
        ax.set_ylabel("Frequency", fontsize=12)
        ax.set_title(f"Distribution of the {results['k']}-th Digit in Base {r}", fontsize=14)
        ax.grid(True, linestyle='--', alpha=0.5)

        # Highlight the bar for the chosen digit 'd'
        d = results["d"]
        if d < len(patches):
            patches[d].set_fc('salmon')
            
        return fig

# ========= 3. APP INSTANTIATION =========
app = App(app_ui, server)

Exercice 12

Three people each choose a number from the interval $[0, 1]$. What is the probability that a triangle with these side lengths exists?

Solution

Three numbers are the side lengths of a triangle if and only if the largest of them does not exceed the sum of the other two. In other words, we need to compute the volume of the region $\{\max\{x,y,z\}\le (x+y+z)/2\}$ inside the unit cube $[0,1]^3$. The complement consists of three disjoint regions $x+y \le z$, $x+z \le y$, and $y+z \le x$. Each of these regions is a tetrahedron with volume $1/6$. Thus, the total volume of the ‘failure’ region is $3 \cdot (1/6) = 1/2$. The probability that the numbers form a triangle is $1-1/2 = 1/2$.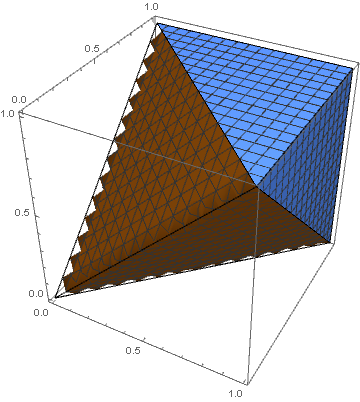

Alternatively, each of the $6$ permutations that orders the three numbers has the same probability. Thus we can compute the measure of the set $\{(x,y,z)\in [0,1]^3 \, :\: x\le y \le z \le x+y\}$, namely \[ p= 6 \int_0^1 dx \int_x^1 dy \int_y^{\min(x+y,1)} dz=6 \int_0^1 dx \int_x^1 (\min(x+y,1)-y) dy = 1/2 \]