Seminar 4

\[\newcommand{\st}{\, : \:} \newcommand{\ind}[1]{\mathbf{1}_{#1}} \newcommand{\dd}{\mathrm{d}}\]

If it is written that a random variable $\xi$ is “given” or “known”, it is implied that its probability measure $\mathbb{P}_\xi$, CDF $F_\xi$, and PDF $p_\xi$ (if the density exists) are known. If you are asked to find the distribution of $\xi$, it is sufficient to find any of the objects mentioned above.

Exercise 1

The distribution of a random vector is given:

\[ \begin{array}{c|c|c|c|c|c} \beta\setminus\alpha & -2 & -1 & 0 & 1 & 2 \\ \hline -2 & 1/32 & 1/32 & 1/24 & 1/32 & 1/32\\ \hline -1 & 1/32 & 1/32 & 1/24 & 1/32 & 1/32\\ \hline 0 & 1/24 & 1/24 & 1/6 & 1/24 & 1/24\\ \hline 1 & 1/32 & 1/32 & 1/24 & 1/32 & 1/32\\ \hline 2 & 1/32 & 1/32 & 1/24 & 1/32 & 1/32\\ \end{array} \]

Find the probability $P(\alpha=\beta)$.
Find the probability $P(\alpha >\beta)$.
Find the probability $P(\alpha\leq \beta)$.
Find the distributions of $\alpha$ and $\beta$.
Is it true that $\alpha$ and $\beta$ are independent?
Find the distribution of $\alpha+\beta$.
Find the distribution of $\alpha\beta$.
Find the distribution of the random vector with components $\alpha+\beta$ and $\alpha-\beta$.
Find the distribution of the random vector with components $\alpha+\beta$ and $\alpha\beta$.

Solution

$\mathbb{P}(\alpha=\beta)$ is the sum of probabilities on the main diagonal: \[ \begin{aligned} \mathbb{P}(\alpha=\beta) = p_{-2,-2} + p_{-1,-1} + p_{0,0} + p_{1,1} + p_{2,2} = \frac{1}{32} + \frac{1}{32} + \frac{1}{6} + \frac{1}{32} + \frac{1}{32} = \frac{4}{32} + \frac{1}{6} = \frac{1}{8} + \frac{1}{6} = \frac{3+4}{24} = \frac{7}{24} \end{aligned} \]
$\mathbb{P}(\alpha > \beta)$ is the sum of all elements above the main diagonal. The table is symmetric, therefore $\mathbb{P}(\alpha > \beta) = \mathbb{P}(\alpha < \beta) =(1 - \mathbb{P}(\alpha=\beta))/2=17/48$.
$\mathbb{P}(\alpha \le \beta) = 1 - \mathbb{P}(\alpha > \beta) = \frac{31}{48}$.
To get the distribution of $\alpha$, sum over columns: e.g. $\mathbb{P}(\alpha=-2) = 4 \cdot \frac{1}{32} + \frac{1}{24} = \frac{1}{6}$. Due to the symmetry of the table, the distribution of $\beta$ (sum over rows) is the same.
No, they are not independent, e.g. $\mathbb{P}(\alpha=-2, \beta=-2) = 1/32 \neq \mathbb{P}(\alpha=-2)\mathbb{P}(\beta=-2) = 1/36$.

To find the distributions of the next points, you need to group the cells of the table (these are tedious but straightforward calculations):

For $\alpha+\beta$: group the cells $(i,j)$ with the same sum $k=i+j$.
For $\alpha\beta$: group the cells with the same product $k=i \cdot j$.
For $(\alpha+\beta, \alpha-\beta)$, this is in bijection with $(\alpha,\beta)$, so each entry corresponds to one entry in the table, i.e. $(\alpha,\beta)=((\alpha+\beta)+(\alpha-\beta),(\alpha+\beta)-(\alpha-\beta))/2$.
For $(\alpha+\beta, \alpha\beta)$, compute the joint law separating the cases where $\alpha$ or $\beta$ vanishes.

Exercise 2 [H]

The distributions of independent random variables $\xi$ and $\eta$ are given:

\[ \begin{array}{c|c|c|c|c|c} \xi & -2 & -1 & 0 & 1 & 2 \\ \hline & 1/4 & 1/8 & 1/4 & 1/8 & 1/4\\ \end{array} \]

\[ \begin{array}{c|c|c|c|c|c} \eta & -2 & -1 & 0 & 1 & 2 \\ \hline & 1/8 & 1/4 & 1/4 & 1/4 & 1/8\\ \end{array} \]

Find the probability $P(\xi=\eta)$.
Find the probability $P(\xi >\eta)$.
Find the probability $P(\xi\leq \eta)$.
Find the distributions of $\xi+\eta$ and $\xi-\eta$.
Find the distribution of $\xi\eta$.
Find the distribution of the random vector with components $\xi+\eta$ and $\xi-\eta$.
Are $\xi+\eta$ and $\xi-\eta$ dependent?
Find the distribution of the random vector with components $\xi+\eta$ and $\xi\eta$.

Solution

$\mathbb{P}(\xi=\eta) = \sum_k \mathbb{P}(\xi=k, \eta=k) = \sum_k \mathbb{P}(\xi=k)\mathbb{P}(\eta=k)= \frac{3}{16}$ due to independence.

Similarly b, c, d, e, f, h. The calculations are performed by considering $\mathbb{P}(\xi=i, \eta=j) = \mathbb{P}(\xi=i)\mathbb{P}(\eta=j)$ and summing the probabilities over the corresponding regions.

Let’s check the independence of $U=\xi+\eta$ and $V=\xi-\eta$. $\mathbb{P}(U=4, V=0) = \mathbb{P}(\xi=2, \eta=2) \neq \mathbb{P}(V=0)\mathbb{P}(U=4)$. The variables $U$ and $V$ are dependent.

Independence of Random Variables

Exercise 3 [H]

Let $\xi\sim \mathrm{Uniform}([0,1])$ and $\eta\sim \mathrm{Bernoulli}(1/3)$. Define these random variables on the same probability space so that they are

independent
dependent.

This means that for each part, you need to devise a probability space and a random vector $\zeta = (\alpha,\beta)$ on it, such that $\mathbb{P}_\alpha = \mathbb{P}_\xi$ and $\mathbb{P}_\eta = \mathbb{P}_\beta$.

Solution

Independent: Take $\Omega = [0,1] \times [0,1]$ with the Lebesgue measure, as the probability space. Set $\alpha(t_1, t_2) = t_1$ and $\beta(t_1, t_2) = \mathbf{1}_{[0, 1/3]}(t_2)$. We can also do the same taking $\Omega=[0,1]\times \{0,1\}$.
Dependent: Take the space $\Omega = [0,1]$ with the Lebesgue measure. Set $\alpha(t) = t$, $\beta(t) = \mathbf{1}_{[0, 1/3]}(t)$.

Exercise 4

Consider the probability space $([0,1], \mathcal{B}([0,1]), \text{Leb})$. Are the following random variables dependent?

$\xi(t)=2t$, $\eta(t)=1-t^2$
$\xi(t)=\operatorname{sign}\left[\sin(2\pi t)\right]$, $\eta(t)=\operatorname{sign}\left[\sin(4\pi t)\right]$
$\xi(t)=\operatorname{sign}\left[\sin(2\pi t)\right]$, $\eta(t)=\operatorname{sign}(t-1/3)$?

Solution

Dependent. They are functionally related: $\eta(t) = 1 - (\xi(t)/2)^2$. If we know the value of $\xi(t)$, we uniquely know the value of $\eta(t)$. For instance for $\varepsilon>0$ small enough, $\mathbb{P}(\xi \le \varepsilon, \eta \le \varepsilon) = 0 \neq \mathbb{P}(\xi \le \varepsilon) \mathbb{P}(\eta \le \varepsilon)>0$.
Independent. $\mathbb{P}(\xi=1 ,\eta=1)=1/4=\mathbb{P}(\xi=1) \mathbb{P}(\eta=1)$, and this is enough since both $\eta$ and $\xi$ only take two values with positive probability.
Dependent. E.g. $\mathbb{P}(\xi =+1 | \eta=-1 )=1 > \mathbb{P}(\xi =+1)$.

Exercise 5 [H]

Provide an example of two discrete random variables that are dependent but not functionally dependent, or explain why such an example does not exist.

Solution

Two random variables $\alpha, \beta$ are called functionally dependent if one is a measurable function of the other, for example $\beta = f(\alpha)$. This means that knowing the value of $\alpha$, we uniquely know the value of $\beta$. This is typically much stronger than just dependency. E.g. in the previous example $\xi(t)=\operatorname{sign}\left[\sin(2\pi t)\right]$, $\eta(t)=\operatorname{sign}(t-1/3)$ are dependent, but not functionally dependent.

Exercise 6 [H]

Is it true that if $\xi$ and $\eta$ are independent, then for any function $f:\mathbb{R}\to\mathbb{R}$, the random variables $f(\xi)$ and $f(\eta)$ are also independent?

Solution

We can even take $f,g$ measurable. Then \[ \mathbb{P}(f(\xi) \in A, g(\eta) \in B) =\mathbb{P}(\xi \in f^{-1}(A), \eta \in g^{-1}(B)) = \mathbb{P}(\xi \in f^{-1}(A)) \mathbb{P}(\eta \in g^{-1}(B))=\mathbb{P}(f(\xi) \in A) \mathbb{P}(g(\eta) \in B) \]

Exercise 7 [H]

Is it true that if $\xi$ and $\eta$ are dependent, then $\xi^2$ and $\eta^2$ must also be dependent?

Solution

In general it is not true that the independence of $f(\xi)$ and $g(\eta)$ implies the independence of $\xi$ and $\eta$. E.g. take $\xi=\eta=2\zeta-1$, where $\zeta \sim \mathrm{Bernoulli}(1/2)$. Then $\xi^2=\eta^2=1$ are independent.

Exercise 8 [H]

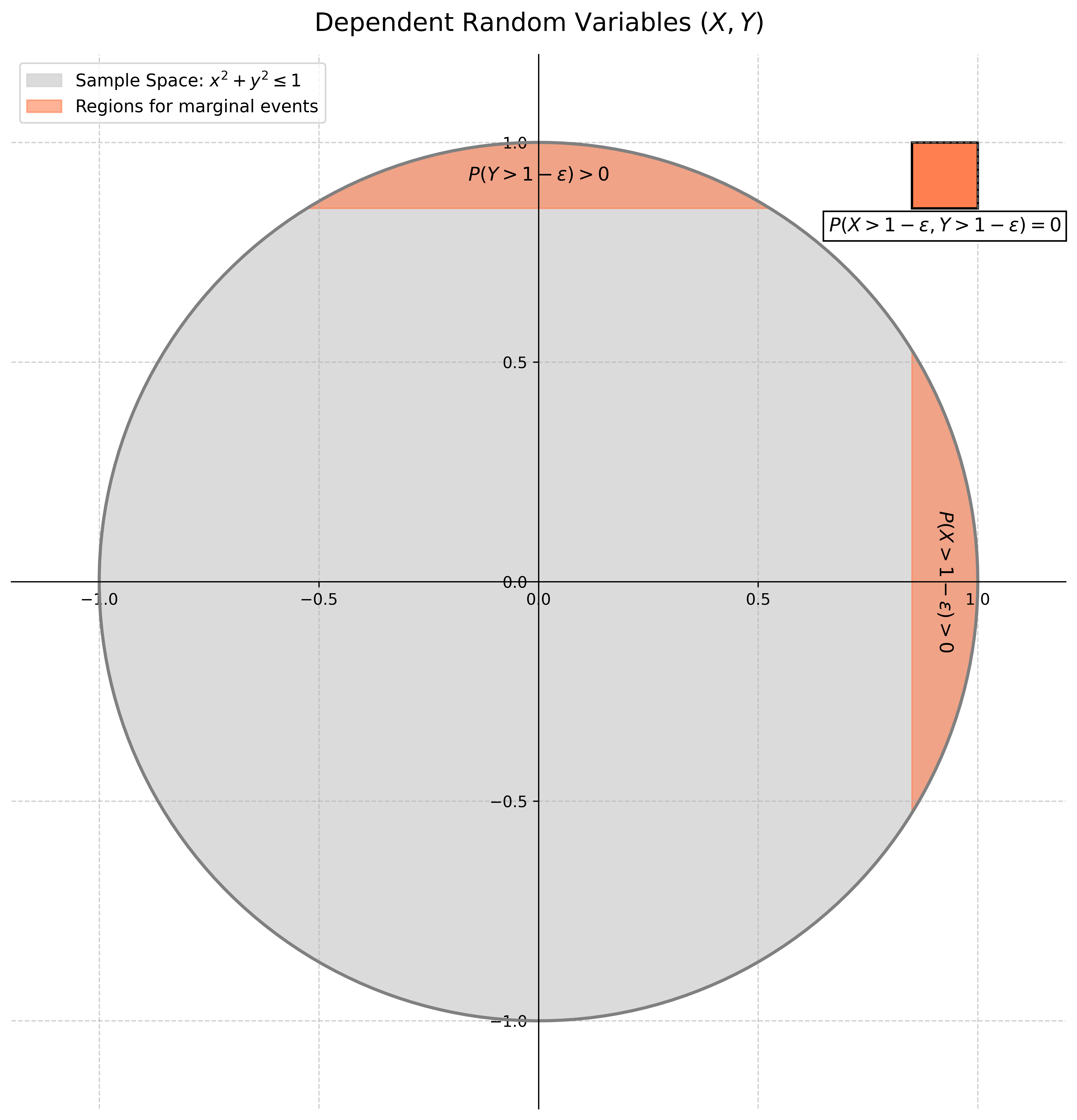
Let the random vector $(\xi,\eta)$ have a uniform distribution in the disk ${(x, y) : x^2+y^2 \le 1}$. Are the random variables $\xi$ and $\eta$ independent?

Solution

No, for instance for $\varepsilon>0$ small enough, $\mathbb{P}(\xi \ge 1-\varepsilon, \eta \ge 1-\varepsilon)=0 \neq \mathbb{P}(\xi \ge 1-\varepsilon) \mathbb{P}(\eta \ge 1-\varepsilon)>0$.

Distribution Function

Exercise 9

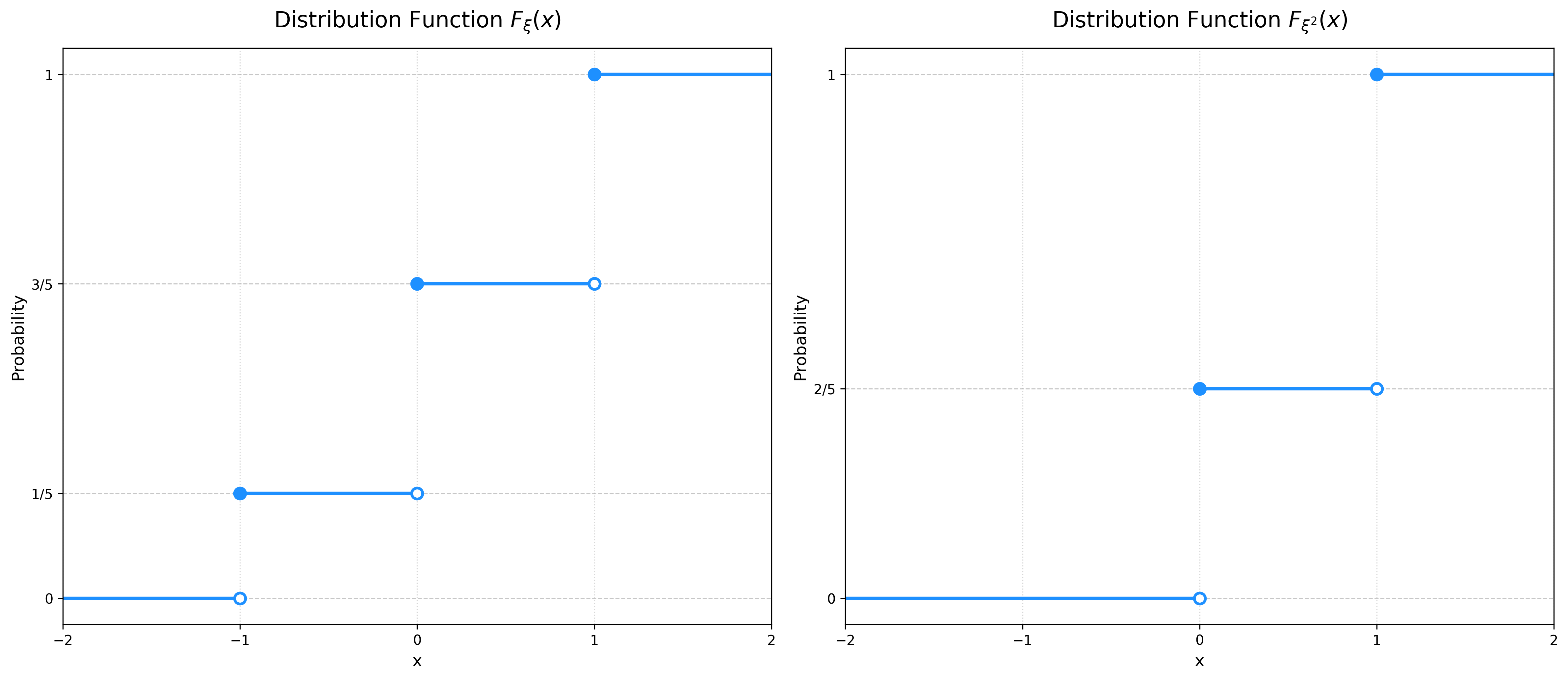
Consider a random variable $\xi$ with the distribution below. Sketch $F_\xi$ and $F_{\xi^2}$.

\[ \begin{array}{c|c|c|c} \xi & -1 & 0 & 1 \\ \hline \mathbb{P}_\xi & 1/5 & 2/5 & 2/5 \\ \end{array} \]

Solution

Exercise 10 [H]

Sketch the distribution function $F_\xi$ for $\xi\sim \mathrm{Poisson}(\lambda), \, \lambda>0$.

Solution

We have that:

$F_\xi(x) = 0$ for $x < 0$.
$F_\xi(x) = e^{-\lambda}$ for $0 \le x < 1$.
$F_\xi(x) = e^{-\lambda}(1+\lambda)$ for $1 \le x < 2$.

and so on. The function approaches 1 as $x \to \infty$.

Exercise 11

A rod of length 2 is broken at a random point. Explicitly define, specifying the probability space, the random variable $\xi$ representing the length of the larger of the two resulting pieces. Find the CDFs $F_\xi$, $F_{\xi^2}$ and the PDFs $p_\xi$, $p_{\xi^2}$.

Solution

Take $\Omega = [0,2]$ with a uniform measure. The break point $U \sim \mathrm{Uniform}([0,2])$, the pieces have lengths $U$ and $2-U$. Thus we are interested in the random variable is $\xi = \max(U, 2-U)$, which takes values in $[1,2]$.

Notice that $\xi \le x \iff 2-x \le U \le x$. Thus for $x\in [1,2]$ \[ F_\xi(x)=\int_{2-x}^x \frac{1}{2} du=x-1 \] So $\xi$ is uniform in $[1,2]$, its density being constant in this interval.

The distribution function of $\xi^2$ is then $F_{\xi^2}(x)= \sqrt{x}-1$ for $x\in [1,4]$, its density being $(2x)^{-1/2} \mathbf{1}_{[1,4]}$.

Exercise 12

Given independent random variables $\xi_1,\dots,\xi_n$, find the distribution function of the random variable

$\max(\xi_1,\dots,\xi_n)$.
$\min(\xi_1,\dots,\xi_n)$.

Solution

Let $F_i(x) = \mathbb{P}(\xi_i \le x)$ be the distribution function for $\xi_i$.

Maximum: Let $M_n = \max(\xi_1, \dots, \xi_n)$, then $\{M_n \le x\}$ iff all the $\xi_i$ are no greater than $x$. Thus by virtue of independence: \[ F_{M_n}(x) = \mathbb{P}(M_n \le x) = \mathbb{P}(\xi_1 \le x, \xi_2 \le x, \ldots, \xi_n \le x) = \prod_{i=1}^n F_{i}(x) \] If all $\xi_i$ are identically distributed with CDF $F(x)$, then $F_{M_n}(x) = (F(x))^n$.
Minimum: $m_n = \min(\xi_1, \dots, \xi_n)$. In this case we reason as above on the complementary event $m_n>x$ to get $F_{m_n}(x) = 1 - \prod_{i=1}^n (1 - F_i(x))$. If all $\xi_i$ are identically distributed with CDF $F(x)$, then $F_{m_n}(x) = 1 - (1 - F(x))^n$.

Exercise 13

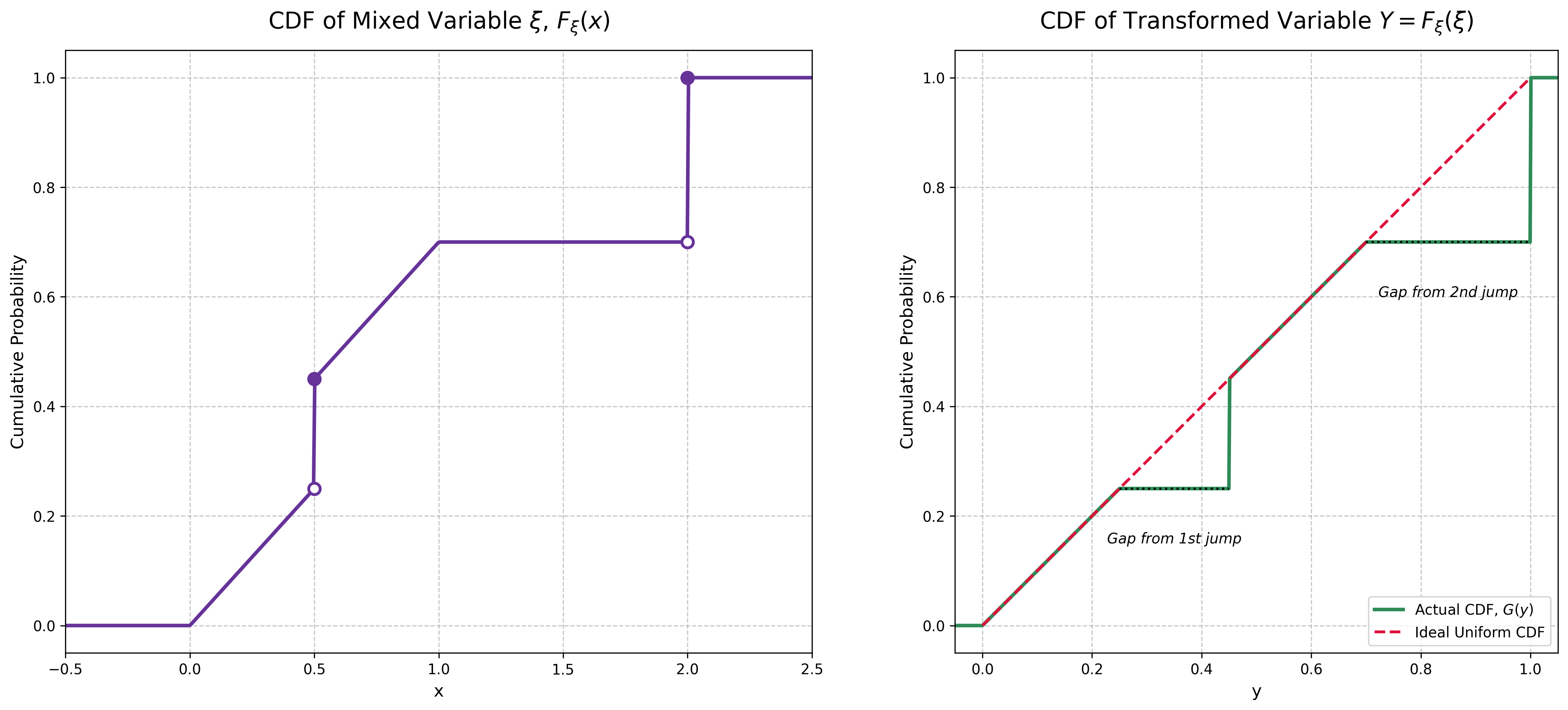
Let the random variable $\xi$ be continuous (i.e., its distribution function $F_\xi$ is continuous). Find the distribution of the random variable $F_\xi(\xi)$.

Solution

Let us denote $F=F_\xi$, to recall that this is not a random function. Let $\eta = F(\xi)$. Since $F$ is a distribution function, its values lie in the interval $[0,1]$. Now $F^{-1}((-\infty,y])$ is an increasing (in $y$) closed subset of $\mathbb{R}$ of the form $F^{-1}((-\infty,y])=(-\infty,s_y]$. Then, by the very definition of $F$ \[ G(y) = \mathbb{P}(\eta \le y)= \mathbb{P}(F(\xi) \le y)= \mathbb{P}(\xi \in F^{-1}((-\infty,y]))= F(s_y) \] If $F$ is continuous, then $G(y)=F(s_y)=y$. Thus $F_\xi(\xi)$ is a uniform random variable. In general, if $F$ is not continuous, $G(y)\le y$.

integral transform with jumps — Figure 1

Exercise 14 [H]

Let $\xi\sim \mathrm{Uniform}([-1,1])$. Find the distribution of the random variable $F_{|\xi|}(\xi)$.

Solution

$|\xi|$ is uniform in $[0,1]$, thus $F_{|\xi|}(\xi)= \max(\xi,0)$. Therefore \[ G(x):= \mathbb{P}(F_{|\xi|}(\xi)\le x)= \begin{cases} 0 & \text{if $x<0$} \\ 1/2+x/2 & \text{if $x\in [0,1]$} \\ 1 & \text{if $x\ge 1$} \end{cases} \]

Exercise 15*

(Mixtures). On a probability space $\Omega$, the following construction depending on a family of random variables $\xi:\mathbb{R}\to\mathbb{R}$ is considered: first, using a random variable $\eta \sim \mathrm{Uniform}([0,1])$, an interval $[0,\eta(\omega)]$ is chosen. Then, independently, a random variable $\zeta(\omega):=\xi_{\eta(\omega)}(\omega)$ is chosen with a given distribution on the interval $[0,\eta(\omega)]$. Find the probability density of the resulting random variable $\xi$, if

$\xi_a \sim \mathrm{Uniform}([0,a])$,
$\xi_a^2 \sim \mathrm{Uniform}([0,a])$.

Solution

We can justify this formula either with measure theory, or using monotonicity in the law of $\xi_a$ to have an explicit bound. In any case \[ \mathbb{P}(\zeta\le x)= \int_0^1 \mathbb{P}(\xi_a \le x)\, da \]

In this case the last formula gives for $x\in (0,1]$ \[ \mathbb{P}(\zeta\le x)= \int_0^1 \tfrac{x}{a} \mathbf{1}_{[0,a)}(x)+ \mathbf{1}_{[a,\infty)}(x) \, da = x-x \log(x) \] which has density $-\log(x) \mathbf{1}_{(0,1]}(x)$.
In this case, for $x\in (0,1)$, $\mathbb{P}(\xi_a \le x)=\mathbb{P}(\xi_a^2 \le x^2)= x^2/a \mathbf{1}_{[0,\sqrt{a})}(x)+ \mathbf{1}_{[\sqrt{a},\infty)}(x)$. Therefore for $x\in (0,1)$ \[ \mathbb{P}(\zeta\le x) = \int_0^1 \tfrac{x^2}{a} \mathbf{1}_{[0,\sqrt{a})}(x)+ \mathbf{1}_{[\sqrt{a},\infty)}(x) da= x^2-2x^2 \log(x) \] and the density is therefore $-4x \log(x) \mathbf{1}_{[0,1]}(x)$, a substantially different behavior around $x=0$.

Exercise 16*

Let $\xi\sim \mathrm{Exp}(\lambda)$. Are its integer and fractional parts independent?

Solution

They are independent. Let $X:= \lfloor \xi \rfloor$ be the integer part, and $\eta: = \xi - \lfloor \xi \rfloor$ be the fractional part. For $k \in \{0,1,2,\dots\}$ and $y \in [0,1)$, we compute the joint distribution \[ \mathbb{P}(X=k, \eta \le y)=\mathbb{P}(k \le \xi \le k+y)= e^{-\lambda k} - e^{-\lambda (k+y)}= e^{-\lambda k}(1-e^{-\lambda y}) \] As this is the product of a function $k$ times a function of $y$, the random variables are independent. We see in particular that $X$ is geometric with (non-success) parameter $e^{-\lambda}$, while $\eta$ has density $\lambda e^{-\lambda y}(1-e^{-\lambda})^{-1} \mathbf{1}_{[0,1]}(y)$.

Additional Exercises

Exercise 17

Let $\xi \colon \Omega \to E$ be a random variable, and $f\colon E\to F$ be measurable. Here $E,F$ are measurable space. Prove that the $(\xi,f(\xi))$ are independent iff $f(\xi)$ is constant a.s.

Solution

If $(\xi,f(\xi))$ are independent, then \[ \mathbb{P}(\xi\in A, f(\xi)\in B)=\mathbb{P}(\xi\in A, \xi \in f^{-1}(B))= \mathbb{P}(\xi\in A) \mathbb{P}(\xi \in f^{-1}(B))=\mathbb{P}(\xi\in A) \mathbb{P}(f(\xi) \in B) \] If we now choose $A=f^{-1}(B)$ we get $\mathbb{P}(f(\xi)\in B)=\mathbb{P}(f(\xi)\in B)^2$. Namely $\mathbb{P}(f(\xi)\in B)\in \{0,1\}$ for all measurable $B$. This is the correct way of saying that $f(\xi)$ is constant. I.e., if the $\sigma$-algebra on $F contains singletons, this means that $f(\xi)$ is constant a.s.. Otherwise, being constant is not defined as a measurable event while saying that the law of $f(\xi)$ takes value in $\{0,1\}$ still makes sense.